Optimal Frequency Warpings
In [269], optimal allpass coefficients ![]() were
computed for sampling rates of twice the Bark band-edge frequencies by
means of four different optimization methods:
were
computed for sampling rates of twice the Bark band-edge frequencies by
means of four different optimization methods:
- Minimize the peak
arc-length error
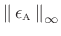 at each sampling rate to obtain
the optimal Chebyshev allpass parameter
at each sampling rate to obtain
the optimal Chebyshev allpass parameter
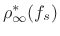 .
.
- Minimize the sum of squared
arc-length errors
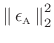 to obtain
the optimal least-squares allpass parameter
to obtain
the optimal least-squares allpass parameter
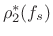 .
.
- Use the closed-form weighted equation-error solution
(E.3.1) computed twice, first with
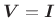 ,
and second with
,
and second with
 set from (E.3.1) to obtain
the optimal ``weighted equation error'' solution
set from (E.3.1) to obtain
the optimal ``weighted equation error'' solution
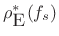 .
.
- Fit the function
![$ \gamma_1\left[{2\over\pi}\arctan(\gamma_2f_s)\right]^{{1\over2}}+\gamma_3 $](http://www.dsprelated.com/josimages_new/sasp2/img2923.png) to the optimal Chebyshev allpass
parameter
to the optimal Chebyshev allpass
parameter
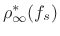 via Chebyshev optimization with respect to
via Chebyshev optimization with respect to
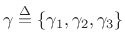 .
We will refer to the resulting function as
the ``arctangent approximation''
.
We will refer to the resulting function as
the ``arctangent approximation''
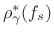 (or, less
formally, the ``Barktan formula''), and note that
it is easily computed directly from the sampling rate.
(or, less
formally, the ``Barktan formula''), and note that
it is easily computed directly from the sampling rate.
![\includegraphics[width=\twidth]{eps/pfs}](http://www.dsprelated.com/josimages_new/sasp2/img2927.png) |
![\includegraphics[width=\twidth]{eps/rmspkerr}](http://www.dsprelated.com/josimages_new/sasp2/img2928.png) |
The peak and rms frequency-mapping errors are plotted versus sampling rate in Fig.E.4. Peak and rms errors in BarksE.1 are plotted for all four cases (Chebyshev, least squares, weighted equation-error, and arctangent approximation). The conformal-map fit to the Bark scale is generally excellent in all cases. We see that the rms error is essentially identical in the first three cases, although the Chebyshev rms error is visibly larger below 10 kHz. Similarly, the peak error is essentially the same for least squares and weighted equation error, with the Chebyshev case being able to shave almost 0.1 Bark from the maximum error at high sampling rates. The arctangent formula shows up to a tenth of a Bark larger peak error at sampling rates 15-30 and 54 kHz, but otherwise it performs very well; at 41 kHz and below 12 kHz the arctangent approximation is essentially optimal in all senses considered.
At sampling rates up to the maximum non-extrapolated sampling rate of ![]() kHz, the peak mapping errors are all much less than one Bark (0.64 Barks
for the Chebyshev case and 0.67 Barks for the two least squares cases).
The mapping errors in Barks can be seen to increase almost linearly with
sampling rate. However, the irregular nature of the Bark-scale data
results in a nonmonotonic relationship at lower sampling rates.
kHz, the peak mapping errors are all much less than one Bark (0.64 Barks
for the Chebyshev case and 0.67 Barks for the two least squares cases).
The mapping errors in Barks can be seen to increase almost linearly with
sampling rate. However, the irregular nature of the Bark-scale data
results in a nonmonotonic relationship at lower sampling rates.
The specific frequency mapping errors versus frequency at the ![]() kHz
sampling rate (the same case shown in Fig.E.1) are plotted in
Fig.E.5. Again, all four cases are overlaid, and again the least
squares and weighted equation-error cases are essentially identical.
By forcing equal and opposite peak errors, the Chebyshev case is able
to lower the peak error from 0.67 to 0.64 Barks. A difference of 0.03
Barks is probably insignificant for most applications. The peak
errors occur at 1.3 kHz and 8.8 kHz where the error is approximately
2/3 Bark. The arctangent formula peak error is 0.73 Barks at 8.8 kHz,
but in return, its secondary error peak at 1.3 kHz is only 0.55 Barks.
In some applications, such as when working with oversampled signals,
higher accuracy at low frequencies at the expense of higher error at
very high frequencies may be considered a desirable tradeoff.
kHz
sampling rate (the same case shown in Fig.E.1) are plotted in
Fig.E.5. Again, all four cases are overlaid, and again the least
squares and weighted equation-error cases are essentially identical.
By forcing equal and opposite peak errors, the Chebyshev case is able
to lower the peak error from 0.67 to 0.64 Barks. A difference of 0.03
Barks is probably insignificant for most applications. The peak
errors occur at 1.3 kHz and 8.8 kHz where the error is approximately
2/3 Bark. The arctangent formula peak error is 0.73 Barks at 8.8 kHz,
but in return, its secondary error peak at 1.3 kHz is only 0.55 Barks.
In some applications, such as when working with oversampled signals,
higher accuracy at low frequencies at the expense of higher error at
very high frequencies may be considered a desirable tradeoff.
We see that the mapping falls ``behind'' a bit as frequency increases
from zero to 1.3 kHz, mapping linear frequencies slightly below the
desired corresponding Bark values; then, the mapping ``catches up,''
reaching an error of 0 Barks near 3 kHz. Above 3 kHz, it gets
``ahead'' slightly, with frequencies in Hz being mapped a little too
high, reaching the positive error peak at 8.8 kHz, after which it
falls back down to zero error at
![]() . (Recall that dc and
half the sampling-rate are always points of zero error by
construction.)
. (Recall that dc and
half the sampling-rate are always points of zero error by
construction.)
![\includegraphics[width=\twidth]{eps/rbe}](http://www.dsprelated.com/josimages_new/sasp2/img2935.png) |
Next Section:
Bark Relative Bandwidth Mapping Error
Previous Section:
Computing








![\includegraphics[width=\twidth]{eps/fme}](http://www.dsprelated.com/josimages_new/sasp2/img2933.png)











