Optimal Bilinear Bark Warping
It turns out that a first-order conformal map (bilinear transform) can provide a surprisingly close match to the Bark frequency scale [268,269]. This is shown in Fig.E.1.
![\includegraphics[width=\twidth]{eps/fitlogf}](http://www.dsprelated.com/josimages_new/sasp2/img2882.png) |
In the following, a simple direct-form expression is developed for the
map parameter ![]() giving the best least-squares fit to a Bark scale
for a chosen sampling rate. As Fig.E.1 shows, the error is so
small that the solution is also very close to the optimal Chebyshev
fit. In fact, the
giving the best least-squares fit to a Bark scale
for a chosen sampling rate. As Fig.E.1 shows, the error is so
small that the solution is also very close to the optimal Chebyshev
fit. In fact, the ![]() optimal warping is within 0.04 Bark of the
optimal warping is within 0.04 Bark of the
![]() optimal warping. Since the experimental uncertainty when
measuring critical bands is on the order of a tenth of a Bark or more
[178,181,251,298],
we consider the optimal Chebyshev and least-squares maps to be
essentially equivalent psychoacoustically.
optimal warping. Since the experimental uncertainty when
measuring critical bands is on the order of a tenth of a Bark or more
[178,181,251,298],
we consider the optimal Chebyshev and least-squares maps to be
essentially equivalent psychoacoustically.
Computing 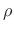
Our goal is to find the allpass coefficient ![]() such that the
frequency mapping
such that the
frequency mapping
best approximates the Bark scale
Using squared frequency errors to gauge the fit between
![]() and
its Bark-warped counterpart, the optimal mapping-parameter
and
its Bark-warped counterpart, the optimal mapping-parameter ![]() may
be written as
may
be written as
![$\displaystyle \rho ^*= \hbox{Arg}\left[\min_{\rho }\left\{\left\Vert\,a(\omega )- b(\omega )\,\right\Vert\right\}\right],
$](http://www.dsprelated.com/josimages_new/sasp2/img2886.png)
where
is nonlinear in
has a norm which is more amenable to minimization. The first issue we address is how the minimizers of
Denote by ![]() and
and ![]() the complex representations of the
frequencies
the complex representations of the
frequencies
![]() and
and
![]() on the unit circle,
on the unit circle,
As seen in Fig.E.2, the absolute frequency error
The desired arc length error
Accordingly, essentially the same
The error
![]() is also nonlinear in the parameter
is also nonlinear in the parameter ![]() , and to find
its norm minimizer, an equation error is introduced, as is
common practice in developing solutions to nonlinear system
identification problems [152]. Consider mapping
the frequency
, and to find
its norm minimizer, an equation error is introduced, as is
common practice in developing solutions to nonlinear system
identification problems [152]. Consider mapping
the frequency
![]() via the allpass transformation
via the allpass transformation
![]() ,
,
Now, multiply (E.3.1) by the denominator
Rearranging terms, we have
where
It is shown in [269] that the optimal weighted least-squares conformal map parameter estimate is given by
If the weighting matrix
![$\displaystyle \frac{\sum_{k=1}^K
v(\omega _k)
\sin\left[\frac{b(\omega_{k})-\omega_{k}}{2}\right]
\sin\left[\frac{b(\omega_{k})+\omega_{k}}{2}\right]
}{\sum_{k=1}^K
v(\omega _k)\sin^2\left[\frac{b(\omega_{k})+\omega_{k}}{2}\right]}$](http://www.dsprelated.com/josimages_new/sasp2/img2913.png) |
|||
![$\displaystyle \frac{\sum_{k=1}^{K}
v(\omega _k)
\left\{\cos\left[b(\omega_{k})\right]- \cos(\omega_{k})\right\}}{%
\sum_{k=1}^{K} v(\omega_{k}) \left\{\cos\left[b(\omega_{k}) + \omega_{k}\right]- 1\right\}}.$](http://www.dsprelated.com/josimages_new/sasp2/img2914.png) |
The kth diagonal element of an optimal diagonal weighting matrix
![]() is given by [269]
is given by [269]
Note that the desired weighting depends on the unknown map parameter
![]() . To overcome this difficulty, we suggest first estimating
. To overcome this difficulty, we suggest first estimating
![]() using
using
![]() , where
, where
![]() denotes the identity matrix,
and then computing
denotes the identity matrix,
and then computing ![]() using the weighting (E.3.1) based on the
unweighted solution. This is analogous to the Steiglitz-McBride
algorithm for converting an equation-error minimizer to the more
desired ``output-error'' minimizer using an iteratively computed
weight function [151].
using the weighting (E.3.1) based on the
unweighted solution. This is analogous to the Steiglitz-McBride
algorithm for converting an equation-error minimizer to the more
desired ``output-error'' minimizer using an iteratively computed
weight function [151].
Optimal Frequency Warpings
In [269], optimal allpass coefficients ![]() were
computed for sampling rates of twice the Bark band-edge frequencies by
means of four different optimization methods:
were
computed for sampling rates of twice the Bark band-edge frequencies by
means of four different optimization methods:
- Minimize the peak
arc-length error
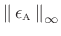 at each sampling rate to obtain
the optimal Chebyshev allpass parameter
at each sampling rate to obtain
the optimal Chebyshev allpass parameter
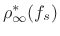 .
.
- Minimize the sum of squared
arc-length errors
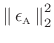 to obtain
the optimal least-squares allpass parameter
to obtain
the optimal least-squares allpass parameter
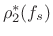 .
.
- Use the closed-form weighted equation-error solution
(E.3.1) computed twice, first with
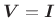 ,
and second with
,
and second with
 set from (E.3.1) to obtain
the optimal ``weighted equation error'' solution
set from (E.3.1) to obtain
the optimal ``weighted equation error'' solution
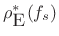 .
.
- Fit the function
![$ \gamma_1\left[{2\over\pi}\arctan(\gamma_2f_s)\right]^{{1\over2}}+\gamma_3 $](http://www.dsprelated.com/josimages_new/sasp2/img2923.png) to the optimal Chebyshev allpass
parameter
to the optimal Chebyshev allpass
parameter
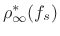 via Chebyshev optimization with respect to
via Chebyshev optimization with respect to
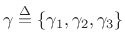 .
We will refer to the resulting function as
the ``arctangent approximation''
.
We will refer to the resulting function as
the ``arctangent approximation''
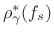 (or, less
formally, the ``Barktan formula''), and note that
it is easily computed directly from the sampling rate.
(or, less
formally, the ``Barktan formula''), and note that
it is easily computed directly from the sampling rate.
![\includegraphics[width=\twidth]{eps/pfs}](http://www.dsprelated.com/josimages_new/sasp2/img2927.png) |
![\includegraphics[width=\twidth]{eps/rmspkerr}](http://www.dsprelated.com/josimages_new/sasp2/img2928.png) |
The peak and rms frequency-mapping errors are plotted versus sampling rate in Fig.E.4. Peak and rms errors in BarksE.1 are plotted for all four cases (Chebyshev, least squares, weighted equation-error, and arctangent approximation). The conformal-map fit to the Bark scale is generally excellent in all cases. We see that the rms error is essentially identical in the first three cases, although the Chebyshev rms error is visibly larger below 10 kHz. Similarly, the peak error is essentially the same for least squares and weighted equation error, with the Chebyshev case being able to shave almost 0.1 Bark from the maximum error at high sampling rates. The arctangent formula shows up to a tenth of a Bark larger peak error at sampling rates 15-30 and 54 kHz, but otherwise it performs very well; at 41 kHz and below 12 kHz the arctangent approximation is essentially optimal in all senses considered.
At sampling rates up to the maximum non-extrapolated sampling rate of ![]() kHz, the peak mapping errors are all much less than one Bark (0.64 Barks
for the Chebyshev case and 0.67 Barks for the two least squares cases).
The mapping errors in Barks can be seen to increase almost linearly with
sampling rate. However, the irregular nature of the Bark-scale data
results in a nonmonotonic relationship at lower sampling rates.
kHz, the peak mapping errors are all much less than one Bark (0.64 Barks
for the Chebyshev case and 0.67 Barks for the two least squares cases).
The mapping errors in Barks can be seen to increase almost linearly with
sampling rate. However, the irregular nature of the Bark-scale data
results in a nonmonotonic relationship at lower sampling rates.
The specific frequency mapping errors versus frequency at the ![]() kHz
sampling rate (the same case shown in Fig.E.1) are plotted in
Fig.E.5. Again, all four cases are overlaid, and again the least
squares and weighted equation-error cases are essentially identical.
By forcing equal and opposite peak errors, the Chebyshev case is able
to lower the peak error from 0.67 to 0.64 Barks. A difference of 0.03
Barks is probably insignificant for most applications. The peak
errors occur at 1.3 kHz and 8.8 kHz where the error is approximately
2/3 Bark. The arctangent formula peak error is 0.73 Barks at 8.8 kHz,
but in return, its secondary error peak at 1.3 kHz is only 0.55 Barks.
In some applications, such as when working with oversampled signals,
higher accuracy at low frequencies at the expense of higher error at
very high frequencies may be considered a desirable tradeoff.
kHz
sampling rate (the same case shown in Fig.E.1) are plotted in
Fig.E.5. Again, all four cases are overlaid, and again the least
squares and weighted equation-error cases are essentially identical.
By forcing equal and opposite peak errors, the Chebyshev case is able
to lower the peak error from 0.67 to 0.64 Barks. A difference of 0.03
Barks is probably insignificant for most applications. The peak
errors occur at 1.3 kHz and 8.8 kHz where the error is approximately
2/3 Bark. The arctangent formula peak error is 0.73 Barks at 8.8 kHz,
but in return, its secondary error peak at 1.3 kHz is only 0.55 Barks.
In some applications, such as when working with oversampled signals,
higher accuracy at low frequencies at the expense of higher error at
very high frequencies may be considered a desirable tradeoff.
We see that the mapping falls ``behind'' a bit as frequency increases
from zero to 1.3 kHz, mapping linear frequencies slightly below the
desired corresponding Bark values; then, the mapping ``catches up,''
reaching an error of 0 Barks near 3 kHz. Above 3 kHz, it gets
``ahead'' slightly, with frequencies in Hz being mapped a little too
high, reaching the positive error peak at 8.8 kHz, after which it
falls back down to zero error at
![]() . (Recall that dc and
half the sampling-rate are always points of zero error by
construction.)
. (Recall that dc and
half the sampling-rate are always points of zero error by
construction.)
![\includegraphics[width=\twidth]{eps/rbe}](http://www.dsprelated.com/josimages_new/sasp2/img2935.png) |
Bark Relative Bandwidth Mapping Error
The slope of the frequency versus warped-frequency curve can be
interpreted as being proportional to critical bandwidth, since a unit
interval (one Bark) on the warped-frequency axis is magnified by the slope
to restore the band to its original size (one critical bandwidth). It is
therefore interesting to look at the relative slope error, i.e., the
error in the slope of the frequency mapping divided by the ideal Bark-map
slope. We interpret this error measure as the relative
bandwidth-mapping error (RBME). The RBME is plotted in Fig.E.6 for
a ![]() kHz sampling rate. The worst case is 21% for the Chebyshev case
and 20% for both least-squares cases. When the mapping coefficient is
explicitly optimized to minimize RBME, the results of Fig.E.7 are
obtained: the Chebyshev peak error drops from 21% down to 18%, while the
least-squares cases remain unchanged at 20% maximum RBME. A 3% change in
RBME is comparable to the 0.03 Bark peak-error reduction seen in
Fig.E.5 when using the Chebyshev norm instead of the
kHz sampling rate. The worst case is 21% for the Chebyshev case
and 20% for both least-squares cases. When the mapping coefficient is
explicitly optimized to minimize RBME, the results of Fig.E.7 are
obtained: the Chebyshev peak error drops from 21% down to 18%, while the
least-squares cases remain unchanged at 20% maximum RBME. A 3% change in
RBME is comparable to the 0.03 Bark peak-error reduction seen in
Fig.E.5 when using the Chebyshev norm instead of the ![]() norm;
again, such a small difference is not likely to be significant in most
applications.
norm;
again, such a small difference is not likely to be significant in most
applications.
![\includegraphics[width=\twidth]{eps/pkrbmeslp}](http://www.dsprelated.com/josimages_new/sasp2/img2937.png) |
Similar observations are obtained at other sampling rates, as shown in Fig.E.8. Near a 10 kHz sampling rate, the Chebyshev RBME is reduced from 17% when minimizing absolute error in Barks (not shown in any figure) to around 12% by explicitly minimizing the RBME, and this is the sampling-rate range of maximum benefit. At 15.2, 19, 41, and 54 kHz sampling rates, the difference is on the order of only 1%. Other cases generally lie between these extremes. The arctangent formula generally falls between the Chebyshev and optimal least-squares cases, except at the highest (extrapolated) sampling rate 54 kHz. The rms error is very similar in all four cases, although the Chebyshev case has a little larger rms error near a 10 kHz sampling rate, and the arctangent case gives a noticeably larger rms error at 54 kHz.
Error Significance
In one study, young normal listeners exhibited a standard deviation in their measured auditory bandwidths (based on notched-noise masking experiments) on the order of 10% of center frequency [178]. Therefore, a 20% peak error in mapped bandwidth (typical for sampling rates approaching 40 kHz) could be considered significant. However, the range of auditory-filter bandwidths measured in 93 young normal subjects at 2 kHz [178] was 230 to 410 Hz, which is -26% to +32% relative to 310 Hz. In [298], 40 subjects were measured, yielding auditory-filter bandwidths between -33% and +65%, with a standard deviation of 18%. It may thus be concluded that a worst-case mapping error on the order of 20%, while probably detectable by ``golden ears'' listeners, lies well within the range of experimental deviations in the empirical measurement of auditory bandwidth.
As a worst-case example of how the 18% peak bandwidth-mapping error in Fig.E.7 might correspond to an audible distortion, consider one critical band of noise centered at the frequency of maximum negative mapping error, scaled to be the same loudness as a single critical band of noise centered at the frequency of maximum positive error. The systematic nature of the mapping error results in a narrowing of the lower band and expansion of the upper band by about 1.7 dB. As a result, over the warped frequency axis, the upper band will be effectively emphasized over the lower band by about 3 dB.
Arctangent Approximations for

This subsection provides further details on the arctangent approximation for the optimal allpass coefficient as a function of sampling rate. Compared with other spline or polynomial approximations, the arctangent form
was found to provide a more parsimonious expression at a given accuracy level. The idea was that the arctangent function provided a mapping from the interval
![$\displaystyle f_s= {1\over \gamma_2}\tan\left[{\pi\over2} \left(\frac{\rho _{\mathbf\gamma}- \gamma_3}{\gamma_1}\right)^2\right].
$](http://www.dsprelated.com/josimages_new/sasp2/img2945.png)
To obtain the optimal arctangent form
![]() , the expression for
, the expression for
![]() in (E.3.5) was optimized with respect to its free
parameters
in (E.3.5) was optimized with respect to its free
parameters
![]() to match the optimal
Chebyshev allpass coefficient as a function of sampling rate:
to match the optimal
Chebyshev allpass coefficient as a function of sampling rate:
![$\displaystyle \rho ^*_{\mathbf\gamma}(f_s) \isdef \hbox{Arg}\left[\min_{{\mathbf\gamma}}\left\{\left\Vert\,\rho ^*_\infty(f_s) - \rho _{\mathbf\gamma}(f_s)\,\right\Vert _\infty\right\}\right].
$](http://www.dsprelated.com/josimages_new/sasp2/img2947.png)
For a Bark warping, the optimized arctangent formula was found to be
where
When the optimality criterion is chosen to minimize relative bandwidth mapping error (relative map slope error), the arctangent formula optimization yields
The performance of this formula is shown in Fig.E.8. It tends to follow the performance of the optimal least squares map parameter even though the peak parameter error was minimized relative to the optimal Chebyshev map. At 54 kHz there is an additional 3% bandwidth error due to the arctangent approximation, and near 10 kHz the additional error is about 4%; at other sampling rates, the performance of the RBME arctangent approximation is better, and like (E.3.5), it is extremely accurate at 41 kHz.
Next Section:
Application to Audio Filter Design
Previous Section:
The Bilinear Transform









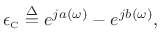
![\includegraphics[width=3in]{eps/eaec}](http://www.dsprelated.com/josimages_new/sasp2/img2893.png)
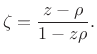
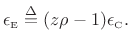
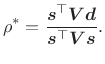
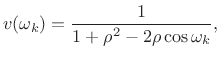
![\includegraphics[width=\twidth]{eps/fme}](http://www.dsprelated.com/josimages_new/sasp2/img2933.png)
![\includegraphics[width=\twidth]{eps/rbeslp}](http://www.dsprelated.com/josimages_new/sasp2/img2936.png)
![$\displaystyle \rho _{\mathbf\gamma}(f_s) \isdef \max\left\{0,\gamma_1\left[{2\over\pi}\arctan(\gamma_2f_s)\right]^{{1\over2}}+\gamma_3 \right\}
$](http://www.dsprelated.com/josimages_new/sasp2/img2938.png)
![$\displaystyle \rho ^*_{\mathbf\gamma}(f_s) = 1.0674\left[{2\over\pi}\arctan(0.06583f_s)\right]^{{1\over2}}-0.1916,
$](http://www.dsprelated.com/josimages_new/sasp2/img2948.png)
![$\displaystyle \rho ^*_{\mathbf\gamma}(f_s) = 1.0480\left[{2\over\pi}\arctan(0.07212f_s)\right]^{{1\over2}}-0.1957.
$](http://www.dsprelated.com/josimages_new/sasp2/img2949.png)











