DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Perfect Reconstruction Cosine Modulated Filter Banks

By changing the phases $ \phi_k$ , the pseudo-QMF filter bank can yield perfect reconstruction:

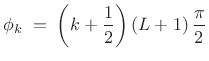$\displaystyle \phi_k \eqsp \left(k+\frac{1}{2}\right)\left(L+1\right)\frac{\pi}{2}$ (12.101)

where $ L$ is the length of the polyphase filter ($ M=LN$ ).

If $ M=2N$ , then this is the oddly stacked Princen-Bradley filter bank and the analysis filters are related by cosine modulations of the lowpass prototype:

$\displaystyle f_k(n) \eqsp h(n)\hbox{cos}\left[\left(n+\frac{N+1}{2}\right)\left(k+\frac{1}{2}\right)\frac{\pi}{N}\right],\quad k=0,\ldots,N-1$ (12.102)

However, the length of the filters $ M$ can be any even multiple of $ N$ :

$\displaystyle M\eqsp LN, \quad (L/2) \in \cal{Z}$ (12.103)

The parameter $ L$ is called the overlapping factor. These filter banks are also referred to as extended lapped transforms, when $ K \ge 2$ [159].

Next Section:
MPEG Layer III Filter Bank
Previous Section:
Pseudo-QMF Cosine Modulation Filter Bank