Pseudo-QMF Cosine Modulation Filter Bank

Free Books Spectral Audio Signal Processing

Section 11.3.5 introduced two-channel quadrature mirror filter banks (QMF). QMFs were shown to provide a particular class of perfect reconstruction filter banks. We found, however, that the quadrature mirror constraint on the analysis filters,

$\displaystyle H_1(z) \eqsp H_0(-z),$

(12.97)

was rather severe in that linear-phase FIR implementations only exist in the two-tap case $H_k(z) = h_{0k}+h_{1k}z^{-1}$ , . In addition to relaxing this constraint, we need to be able to design an -channel filter bank for any .

The Pseudo-QMF (PQMF) filter bank is a ``near perfect reconstruction'' filter bank in which aliasing cancellation occurs only between adjacent bands [194,287]. The PQMF filters commonly used in perceptual audio coders employ bandpass filters with stop-band attenuation near dB, so the neglected bands (which alias freely) are not significant. An outline of the design procedure is as follows:

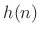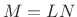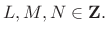
Design a lowpass prototype window, , with length , $L,M,N \in {\bf Z}.$
The lowpass design is constrained to give aliasing cancellation in neighboring subbands:

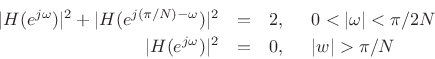
$\begin{eqnarray*} \vert H(e^{j\omega})\vert^2 + \vert H(e^{j(\pi/N)-\omega})\vert^2 &=& 2, \hspace{.5cm}0 < \vert\omega\vert < \pi/{2N} \\ \vert H(e^{j\omega})\vert^2 &=& 0, \hspace{.5cm}\vert w\vert > \pi/N \end{eqnarray*}$
The filter bank analysis filters 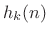are cosine modulations of :

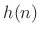$\displaystyle h_k(n) \eqsp h(n)\hbox{cos}\left[\left(k+\frac{1}{2}\right)\left(n-\frac{M-1}{2}\right)\frac{\pi}{N} + \phi_k\right],$ (12.98)

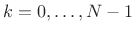$k=0,\ldots,N-1$ , where the phases are restricted according to

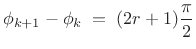
$\displaystyle \phi_{k+1} - \phi_k \eqsp (2r+1)\frac{\pi}{2}$ (12.99)

again for aliasing cancellation.
Since it is an orthogonal filter bank by construction, the synthesis filters are simply the time-reverse of the analysis filters:

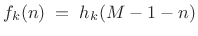
$\displaystyle f_k(n) \eqsp h_k(M-1-n)$ (12.100)