DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Peak Detection (Steps 3 and 4)

Due to the sampled nature of spectra obtained using the STFT, each peak (location and height) found by finding the maximum-magnitude frequency bin is only accurate to within half a bin. A bin represents a frequency interval of $ f_s/N$ Hz, where $ N$ is the FFT size. Zero-padding increases the number of FFT bins per Hz and thus increases the accuracy of the simple peak detection. However, to obtain frequency accuracy on the level of $ 0.1\%$ of the distance from a sinc maximum to its first zero crossing (in the case of a rectangular window), the zero-padding factor required is $ 1000$ . (Note that with no zero padding, the STFT analysis parameters are typically arranged so that the distance from the sinc peak to its first zero-crossing is equal to the fundamental frequency of a harmonic sound. Under these conditions, $ 0.1\%$ of this interval is equal to the relative accuracy in the fundamental frequency measurement. Thus, this is a realistic specification in view of pitch discrimination accuracy.) Since we would nominally take two periods into the data frame (for a Rectangular window), a $ 100$ Hz sinusoid at a sampling rate of $ 50$ KHz would have a period of $ 50,000/100=500$ samples, so that the FFT size would have to exceed one million. A more efficient spectral interpolation scheme is to zero-pad only enough so that quadratic (or other simple) spectral interpolation, using only bins immediately surrounding the maximum-magnitude bin, suffices to refine the estimate to $ 0.1\%$ accuracy. PARSHL uses a parabolic interpolator which fits a parabola through the highest three samples of a peak to estimate the true peak location and height (cf. Fig.H.2).

Figure H.2: Parabolic interpolation of the highest three samples of a peak.
\includegraphics[width=\twidth]{eps/fig4}

Figure H.3: Coordinate system for the parabolic interpolation.
\includegraphics[width=\twidth]{eps/fig5}

We have seen that each sinusoid appears as a shifted window transform which is a sinc-like function. A robust method for estimating peak frequency with very high accuracy would be to fit a window transform to the sampled spectral peaks by cross-correlating the whole window transform with the entire spectrum and taking and interpolated peak location in the cross-correlation function as the frequency estimate. This method offers much greater immunity to noise and interference from other signal components.

To describe the parabolic interpolation strategy, let's define a coordinate system centered at $ (k_\beta ,0)$ , where $ k_\beta $ is the bin number of the spectral magnitude maximum, i.e., $ \tilde{x}_m^\prime (e^{j\omega_{k_\beta}})\geq \tilde{x}_m^\prime (e^{j\omega_k })$ for all $ k\neq k_\beta $ . An example is shown in Figure 4. We desire a general parabola of the form

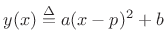$\displaystyle y(x) \isdef a(x-p)^2 + b$ (H.2)

such that $ y(-1) = \alpha$ , $ y(0) = \beta$ , and $ y(1) = \gamma$ , where $ \alpha $ , $ \beta $ , and $ \gamma$ are the values of the three highest samples:
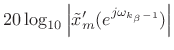$\displaystyle \alpha$ $\displaystyle \isdef$ $\displaystyle 20\log_{10}\left\vert\tilde{x}_m^\prime (e^{j\omega_{k_\beta-1}})\right\vert$ (H.3)
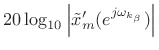$\displaystyle \beta$ $\displaystyle \isdef$ $\displaystyle 20\log_{10}\left\vert\tilde{x}_m^\prime (e^{j\omega_{k_\beta}})\right\vert$ (H.4)
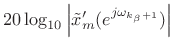$\displaystyle \gamma$ $\displaystyle \isdef$ $\displaystyle 20\log_{10}\left\vert\tilde{x}_m^\prime (e^{j\omega_{k_\beta+1}})\right\vert$ (H.5)

We have found empirically that the frequencies tend to be about twice as accurate when dB magnitude is used rather than just linear magnitude. An interesting open question is what is the optimum nonlinear compression of the magnitude spectrum when quadratically interpolating it to estimate peak locations.

Solving for the parabola peak location $ p$ , we get

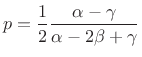$\displaystyle p={1\over 2}{{\alpha - \gamma}\over{\alpha - 2\beta + \gamma}}$ (H.6)

and the estimate of the true peak location (in bins) will be

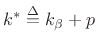$\displaystyle k^\ast \isdef k_\beta +p$ (H.7)

and the peak frequency in Hz is $ f_s k^\ast /N$ . Using $ p$ , the peak height estimate is then

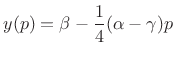$\displaystyle y(p) = \beta - {1\over 4} (\alpha - \gamma) p$ (H.8)

The magnitude spectrum is used to find $ p$ , but $ y(p)$ can be computed separately for the real and imaginary parts of the complex spectrum to yield a complex-valued peak estimate (magnitude and phase).

Once an interpolated peak location has been found, the entire local maximum in the spectrum is removed. This allows the same algorithm to be used for the next peak. This peak detection and deletion process is continued until the maximum number of peaks specified by the user is found.

Next Section:
Peak Matching (Step 5)
Previous Section:
Filling the FFT Input Buffer (Step 2)