Rectangular Pulse
The rectangular pulse of width ![]() centered on time 0 may be
defined by
centered on time 0 may be
defined by
![$\displaystyle p_\tau(t) \isdef \left\{\begin{array}{ll} 1, & \left\vert t\right\vert\leq\frac{\tau}{2} \\ [5pt] 0, & \left\vert t\right\vert>\frac{\tau}{2}. \\ \end{array} \right.$](http://www.dsprelated.com/josimages_new/sasp2/img2465.png) |
(B.31) |
Its Fourier transform is easily evaluated:
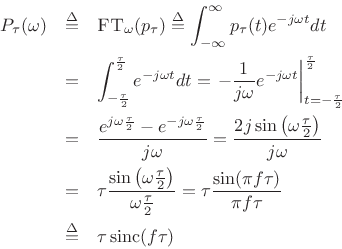
Thus, we have derived the Fourier pair
Note that sinc
| (B.33) |
From this, the scaling theorem implies the more general case:
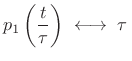 sinc sinc |
(B.34) |
Next Section:
Sinc Impulse
Previous Section:
Gaussian Pulse




















