DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Sinc Impulse

The preceding Fourier pair can be used to show that

$\displaystyle \zbox {\lim_{\tau\to\infty} \tau\,\mbox{sinc}(f\tau) = \delta(f).}$ (B.35)


Proof: The inverse Fourier transform of $ \tau\,$sinc$ (f\tau)$ is

\begin{eqnarray*} p_\tau(t) &=& \ensuremath{\int_{-\infty}^{\infty}}\tau\,\mbox{sinc}\left(\frac{\omega}{2\pi}\tau\right) e^{j\omega t}\frac{d\omega}{2\pi}\\ &=& \ensuremath{\int_{-\infty}^{\infty}}\tau\,\mbox{sinc}(f\tau) e^{j2\pi f t}df\\ &=& \left\{\begin{array}{ll} 1, & \left\vert\tau\right\vert\leq 1/2 \\ [5pt] 0, & \mbox{otherwise}. \\ \end{array} \right. \end{eqnarray*}

In particular, in the middle of the rectangular pulse at $ t=0$ , we have

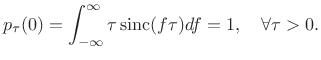$\displaystyle p_\tau(0)=\ensuremath{\int_{-\infty}^{\infty}}\tau\,\mbox{sinc}(f\tau) df = 1, \quad \forall \tau>0.$ (B.36)

This establishes that the algebraic area under $ \tau\,$sinc$ (\tau f)$ is 1 for every $ \tau>0$ . Every delta function (impulse) must have this property.

We now show that $ \tau\,$sinc$ (f\tau)$ also satisfies the sifting property in the limit as $ \tau\to\infty$ . This property fully establishes the limit as a valid impulse. That is, an impulse $ \delta(t)$ is any function having the property that

$\displaystyle \ensuremath{\int_{-\infty}^{\infty}}g(t)\delta(t)dt = \left<g,\delta\right> = g(0)$ (B.37)

for every continuous function $ g(t)$ . In the present case, we need to show, specifically, that

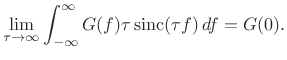$\displaystyle \lim_{\tau\to\infty}\ensuremath{\int_{-\infty}^{\infty}}G(f)\tau\,\mbox{sinc}(\tau f)\,df = G(0).$ (B.38)

Define 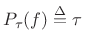$ P_\tau(f)\isdef \tau\,$sinc$ (f\tau)$ . Then by the power theorem (§B.9),

$\displaystyle \left<G,P_\tau\right> = \left<g,p_\tau\right> = \ensuremath{\int_{-\infty}^{\infty}}g(t) p_\tau(t)\,dt = \int_{-\tau/2}^{\tau/2} g(t)\,dt.$ (B.39)

Then as $ \tau\to\infty$ , the limit converges to the algebraic area under $ g$ , which is $ G(0)$ as desired:

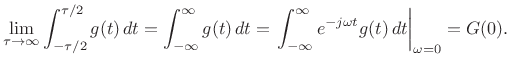$\displaystyle \lim_{\tau\to\infty}\int_{-\tau/2}^{\tau/2} g(t)\,dt = \ensuremath{\int_{-\infty}^{\infty}}g(t)\,dt = \left.\ensuremath{\int_{-\infty}^{\infty}}e^{-j\omega t} g(t)\,dt \right\vert _{\omega=0} = G(0).$ (B.40)

We have thus established that

$\displaystyle {\lim_{\tau\to\infty}\tau\,\mbox{sinc}(f\tau) = \delta(f),}$ (B.41)

where

sinc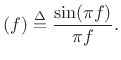$\displaystyle (f)\isdef \frac{\sin(\pi f)}{\pi f}.$ (B.42)

For related discussion, see [36, p. 127].

Next Section:
Impulse Trains
Previous Section:
Rectangular Pulse