DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Gaussian Pulse

The Gaussian pulse of width (second central moment) $ \sigma $ centered on time 0 may be defined by

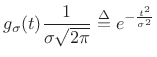$\displaystyle g_\sigma(t) \frac{1}{\sigma\sqrt{2\pi}}\isdef e^{-\frac{t^2}{\sigma^2}}$ (B.29)

where the normalization scale factor is chosen to give unit area under the pulse. Its Fourier transform is derived in Appendix D to be

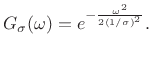$\displaystyle G_\sigma(\omega) = e^{-\frac{\omega^2}{2(1/\sigma)^2}}.$ (B.30)

Next Section:
Rectangular Pulse
Previous Section:
The Continuous-Time Impulse