DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Repeat (Scaling) Operator

We define the repeat operator in the frequency domain as a scaling of frequency axis by some integer factor $ L>0$ :

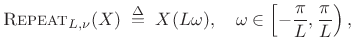$\displaystyle \hbox{\sc Repeat}_{L,\nu}(X) \isdefs X(L\omega), \quad \omega\in\left[-\frac{\pi}{L},\frac{\pi}{L}\right),$ (3.30)

where $ \nu=L\omega\in[-\pi,\pi)$ denotes the radian frequency variable after applying the repeat operator.

The repeat operator maps the entire unit circle (taken as $ -\pi$ to $ \pi$ ) to a segment of itself $ [-\pi/L,\pi/L)$ , centered about $ \omega = 0$ , and repeated $ L$ times. This is illustrated in Fig.2.2 for $ L=3$ .

\begin{psfrags} % latex2html id marker 7156\psfrag{w}{\Large $\omega$}\begin{figure}[htbp] \includegraphics[width=\twidth]{eps/repeat2} \caption{Illustration of the repeat operator.} \end{figure} \end{psfrags}

Since the frequency axis is continuous and $ 2\pi$ -periodic for DTFTs, the repeat operator is precisely equivalent to a scaling operator for the Fourier transform case (§B.4). We call it ``repeat'' rather than ``scale'' because we are restricting the scale factor to positive integers, and because the name ``repeat'' describes more vividly what happens to a periodic spectrum that is compressively frequency-scaled over the unit circle by an integer factor.

Next Section:
Stretch/Repeat (Scaling) Theorem
Previous Section:
Stretch Operator