DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Sample Variance


Definition: The sample variance of a set of $ N$ samples from a particular realization of a stationary stochastic process $ v$ is defined as average squared magnitude after removing the known mean:

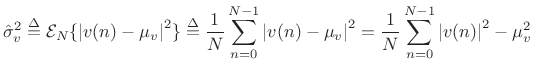$\displaystyle \hat{\sigma}^2_{v} \isdef {\cal E}_N\{\left\vert v(n)-\mu_v\right\vert^2\} \isdef \frac{1}{N}\sum_{n=0}^{N-1} \left\vert v(n)-\mu_v\right\vert^2 = \frac{1}{N}\sum_{n=0}^{N-1} \left\vert v(n)\right\vert^2 -\mu_v^2$ (C.20)

The sample variance is a unbiased estimator of the true variance when the mean is known, i.e.,

$\displaystyle E\{\hat{\sigma}^2_{v}\} = \sigma^2_v.$ (C.21)

This is easy to show by taking the expected value:
$\displaystyle E\{\hat{\sigma}^2_{v}\}$ $\displaystyle =$ $\displaystyle E{\cal E}_N\{\left\vert v(n)-\mu_v\right\vert^2\} = {\cal E}_N\{E\left\vert v(n)-\mu_v\right\vert^2\}$  
  $\displaystyle =$ $\displaystyle {\cal E}_N\{E\left\vert v(n)\right\vert^2-E\overline{v(n)}\mu_v-Ev(n)\overline{\mu_v}+\left\vert\mu_v\right\vert^2\}$  
  $\displaystyle =$ $\displaystyle {\cal E}_N\{\sigma_v^2+\left\vert\mu_v\right\vert^2-\overline{\mu_v}\mu_v-\mu_v\overline{\mu_v}+\left\vert\mu_v\right\vert^2\}$  
  $\displaystyle =$ $\displaystyle {\cal E}_N\{\sigma_v^2\} = \sigma^2_v. \protect$ (C.22)

When the mean is unknown, the sample mean is used in its place:

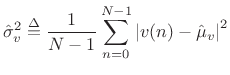$\displaystyle \hat{\sigma}^2_{v} \isdef \frac{1}{N-1}\sum_{n=0}^{N-1} \left\vert v(n)-\hat{\mu}_v\right\vert^2$ (C.23)

The normalization by $ N-1$ instead of $ N$ is necessary to make the sample variance be an unbiased estimator of the true variance. This adjustment is necessary because the sample mean is correlated with the term $ v(n)$ in the sample variance expression. This is revealed by replacing $ \mu_v$ with $ \hat{\mu}_v$ in the calculation of (C.22).

Next Section:
Cross-Correlation
Previous Section:
Variance