Shift Theorem
The shift theorem for Fourier transforms states that
delaying a signal ![]() by
by ![]() seconds multiplies its Fourier
transform by
seconds multiplies its Fourier
transform by
![]() .
.
Proof:
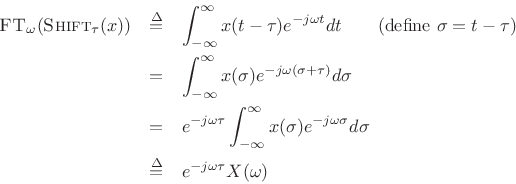
Thus,
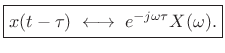 |
(B.12) |
Next Section:
Modulation Theorem (Shift Theorem Dual)
Previous Section:
Scaling Theorem




















