DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Modulation Theorem (Shift Theorem Dual)

The Fourier dual of the shift theorem is often called the modulation theorem:

$\displaystyle \zbox {x(t)e^{j\nu t}\;\longleftrightarrow\;X(\omega-\nu)}$ (B.13)

This is proved in the same way as the shift theorem above by starting with the inverse Fourier transform of the right-hand side:

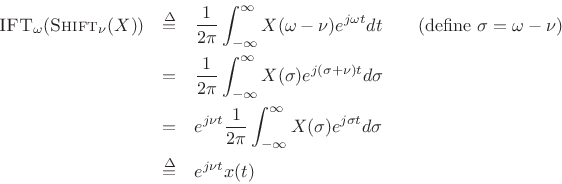
\begin{eqnarray*} \hbox{\sc IFT}_\omega(\hbox{\sc Shift}_\nu(X)) &\isdef & \frac{1}{2\pi}\int_{-\infty}^\infty X(\omega-\nu) e^{j\omega t}dt\qquad\mbox{(define $\sigma=\omega-\nu$)}\\ &=& \frac{1}{2\pi}\int_{-\infty}^\infty X(\sigma) e^{j(\sigma+\nu)t}d\sigma\\ &=& e^{j\nu t}\frac{1}{2\pi}\int_{-\infty}^\infty X(\sigma) e^{j\sigma t}d\sigma\\ &\isdef & e^{j\nu t} x(t) \end{eqnarray*}

or,

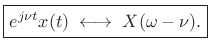$\displaystyle \zbox {e^{j\nu t} x(t) \;\longleftrightarrow\; X(\omega-\nu).}$ (B.14)

Next Section:
Convolution Theorem
Previous Section:
Shift Theorem