DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

TSM by Resampling STFTs Across Time

In view of Chapter 8, a natural implementation of TSM based on the STFT is as follows:

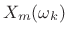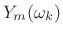  1. Perform a short-time Fourier transform (STFT) using hop size $ R$ . Denote the STFT at frame $ m$ and bin $ k$ by $ X_m(\omega_k)$ , and denote the result of TSM processing by $ Y_m(\omega_k)$ .

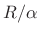  2. To perform TSM by the factor $ \alpha>1$ , advance the ``frame pointer'' $ m$ by $ R/\alpha$ during resynthesis instead of the usual $ R$ samples.

For example, if $ \alpha=2$ ($ 2\times $ slow-down), the first STFT frame $ X_0(\omega_k)$ is processed normally, so that $ Y_0=X_0$ . However, the second output frame $ Y_{1/2}$ corresponds to a time $ m=1/2$ , half way between the first two frames. This output frame may be created by interpolating (across time) the STFT magnitude magnitude spectra of the first. For example, using simple linear interpolation gives

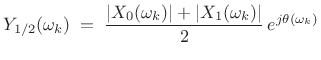$\displaystyle Y_{1/2}(\omega_k) \eqsp \frac{\left\vert X_0(\omega_k)\right\vert + \left\vert X_1(\omega_k)\right\vert}{2} \,e^{j\theta(\omega_k)}$ (11.23)

where the phase $ \theta(\omega_k)$ is chosen to preserve continuity and/or the amplitude envelope from frame to frame under the overlap-add (more on this below). Generalizing to arbitrary TSM factors $ \alpha $ , we obtain

$\displaystyle Y_{m}(\omega_k) \eqsp \left[ (1-\eta)\, \vert X_{\left\lfloor m\right\rfloor }(\omega_k)\vert + \eta\,\vert X_{\left\lceil m\right\rceil }(\omega_k)\vert \right]\, e^{j\theta_m(\omega_k)}$ (11.24)

where $ \eta\isdeftext m-\lfloor m\rfloor $ , and $ m$ is advanced by $ R/\alpha$ each frame-step.

In general, TSM methods based on STFT modification are classified as ``vocoder'' type methods (§G.5). Thus, the TSM implementation outlined above may be termed a weighted overlap-add (WOLA) phase-vocoder method.

Next Section:
Phase Continuation
Previous Section:
TSM and S+N+T