Free Books
   Free Books    Spectral Audio Signal Processing  

Time Reversal

For any complex signal $ x(n)$ , $ n\in(-\infty,\infty)$ , we have

$\displaystyle \zbox {\hbox{\sc Flip}(x) \;\longleftrightarrow\;\hbox{\sc Flip}(X)}$ (3.11)

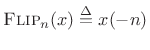where $ \hbox{\sc Flip}_n(x)\isdef x(-n)$ .


Proof:

\begin{eqnarray*} \hbox{\sc DTFT}_\omega(\hbox{\sc Flip}(x)) &\isdef & \sum_{n=-\infty}^{\infty} x(-n)e^{-j\omega n} \eqsp \sum_{m=\infty}^{-\infty} x(m)e^{-j(-\omega) m} \eqsp X(-\omega) \\ [5pt] &\isdef & \hbox{\sc Flip}_\omega(X) \end{eqnarray*}

Arguably, $ \hbox{\sc Flip}(x)$ should include complex conjugation. Let

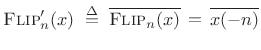$\displaystyle \hbox{\sc Flip}_n'(x)\isdefs \overline{\hbox{\sc Flip}_n(x)}\,\mathrel{\mathop=}\,\overline{x(-n)}$ (3.12)

denote such a definition. Then in this case we have

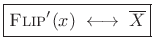$\displaystyle \zbox {\hbox{\sc Flip}'(x) \;\longleftrightarrow\;\overline{X}}$ (3.13)


Proof:

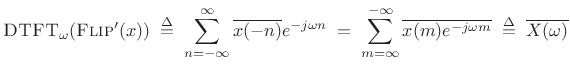$\displaystyle \hbox{\sc DTFT}_\omega(\hbox{\sc Flip}'(x)) \isdefs \sum_{n=-\infty}^{\infty} \overline{x(-n)}e^{-j\omega n} \eqsp \sum_{m=\infty}^{-\infty} \overline{x(m)e^{-j\omega m}} \isdefs \overline{X(\omega)}$ (3.14)

In the typical special case of real signals ( $ x(n)\in{\bf R}$ ), we have $ \hbox{\sc Flip}(x)=\hbox{\sc Flip}'(x)$ so that

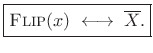$\displaystyle \zbox {\hbox{\sc Flip}(x) \;\longleftrightarrow\;\overline{X}.}$ (3.15)

That is, time-reversing a real signal conjugates its spectrum.

Next Section:
Symmetry of the DTFT for Real Signals
Previous Section:
Linearity of the DTFT