Two-Channel Case

The simplest nontrivial case is channels. Starting with a general linear time-invariant filter

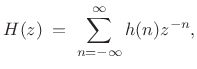$\displaystyle H(z) \eqsp \sum_{n=-\infty}^{\infty}h(n)z^{-n},$

(12.6)

we may separate the even- and odd-indexed terms to get

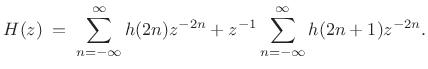$\displaystyle H(z) \eqsp \sum_{n=-\infty}^{\infty}h(2n)z^{-2n} + z^{-1}\sum_{n=-\infty}^{\infty}h(2n+1)z^{-2n}.$

(12.7)

We define the polyphase component filters as follows:

$\begin{eqnarray*} E_0(z)&=&\sum_{n=-\infty}^{\infty}h(2n)z^{-n}\\ [5pt] E_1(z)&=&\sum_{n=-\infty}^{\infty}h(2n+1)z^{-n} \end{eqnarray*}$

and are the polyphase components of the polyphase decomposition of for .

Now write in terms of its polyphase components:

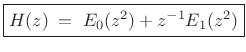$\displaystyle \zbox {H(z) \eqsp E_0(z^2) + z^{-1}E_1(z^2)}$

(12.8)

As a simple example, consider

$\displaystyle H(z)\eqsp 1 + 2z^{-1} + 3z^{-2} + 4z^{-3}.$

(12.9)

Then the polyphase component filters are

$\begin{eqnarray*} E_0(z) &=& 1 + 3z^{-1}\\ [5pt] E_1(z) &=& 2 + 4z^{-1} \end{eqnarray*}$

and

$\displaystyle H(z) \eqsp E_0(z^2) + z^{-1}E_1(z^2) \eqsp (1 + 3z^{-2}) + (2z^{-1} + 4z^{-3}).$

(12.10)

Next Section:
N-Channel Polyphase Decomposition
Previous Section:
Filtering and Downsampling

Sign in