Computing FFT Twiddle Factors
Some days ago I read a post on the comp.dsp newsgroup and, if I understood the poster's words, it seemed that the poster would benefit from knowing how to compute the twiddle factors of a radix-2 fast Fourier transform (FFT).
Then, later it occurred to me that it might be useful for this blog's readers to be aware of algorithms for computing FFT twiddle factors. So,... what follows are two algorithms showing how to compute the individual twiddle factors of an N-point decimation-in-frequency (DIF) and an N-point decimation-in-time (DIT) FFT.
The vast majority of FFT applications use (notice how I used the word "use" instead of the clumsy word "utilize") standard, pre-written, FFT software routines. However, there are non-standard FFT applications (for example, specialized harmonic analysis, transmultiplexers, or perhaps using an FFT to implement a bank of filters) where only a subset of the full N-sample complex FFT results are required. Those oddball FFT applications, sometimes called "pruned FFTs", require computation of individual FFT twiddle factors, and that's the purpose of this blog.
(If, by chance, the computation of FFT twiddle factors is of no interest to you, you might just scroll down to the "A Little History of the FFT" part of this blog.)
Before we present the two twiddle factor computation algorithms, let's understand the configuration of a single "butterfly" operation used in our radix-2 FFTs. We've all seen the signal flow drawings of FFTs with their arrays of butterfly operations. There are various ways of implementing a butterfly operation, but my favorites are the efficient single-complex-multiply butterflies shown in Figure 1. A DIF butterfly is shown in Figure 1(a), while a DIT butterfly is shown in Figure 1(b). In Figure 1 the twiddle factors are shown as e–j2πQ/N, where variable Q is merely an integer in the range of 0 ≤ Q ≤ (N/2)–1.
To simplify this blog's follow-on figures, we'll use Figures 1(c) and 1(d) to represent the DIF and DIT butterflies. As such, Figure 1(c) is equivalent to Figure 1(a), and Figure 1(d) is equivalent to Figure 1(b).
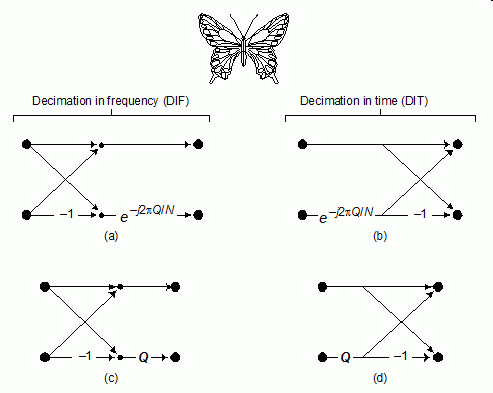
Figure 1: Single-complex-multiply DIF and DIT butterflies.
Computing DIF Twiddle Factors
Take a look at Figure 2 showing the butterfly operations for an 8-point radix-2 DIF FFT.
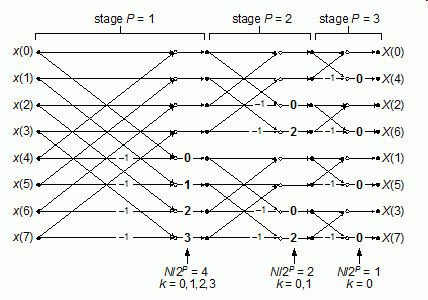
Figure 2: 8-point DIF FFT signal flow diagram.
For the radix-2 DIF FFT using the Figures 1(c) and 1(d) butterflies,
- The N-point DIF FFT has log2(N) stages, numbered P = 1, 2, ..., log2(N).
- Each stage comprises N/2 butterflies.
- Not counting the –1 twiddle factors, the Pth stage has N/2P unique twiddle factors, numbered k = 0, 1, 2, ..., N/2P–1 as indicated by the bold numbers above the upward-pointing arrows at the bottom of Figure 2.
Given those characteristics, the kth unique twiddle factor phase angle for the Pth stage is computed using:
kth DIF twiddle factor angle = k•2P/2 (1)
where 0 ≤ k ≤ N/2P–1. For example, for the second stage (P = 2) of an N = 8-point DIF FFT, the unique Q factors are:
k = 0, Q = 0•2P/2 = 0•4/2 = 0
k = 1, Q = 1•2P/2 = 1•4/2 = 2.
Computing DIT Twiddle Factors
Here's an algorithm for computing the individual twiddle factor angles of a radix-2 DIT FFT. Consider Figure 3 showing the butterfly signal flow of an 8-point DIT FFT.

Figure 3: 8-point DIT FFT signal flow diagram.
For the DIT FFT using the Figures 1(c) and 1(d) butterflies,
- The N-point DIT FFT has log2(N) stages, numbered P = 1, 2, ..., log2(N).
- Each stage comprises N/2 butterflies.
- Not counting the –1 twiddle factors, the Pth stage has N/2 twiddle factors, numbered k = 0, 1, 2, ..., N/2–1 as indicated by the upward arrows at the bottom of Figure 3.
Given those characteristics, the kth DIT twiddle Q factor for the Pth stage is computed using:
kth DIT twiddle factor Q = [⌊k2P/N⌋]bit-rev (2)
where 0 ≤ k ≤ N/2–1. The ⌊q⌋ operation means the integer part of q. The [z]bit-rev function represents the three-step operation of:
[1] convert decimal integer z to a binary number represented by log2(N)–1 binary bits,
[2] perform bit reversal on the binary number as discussed in Section 4.5, and
[3] convert the bit reversed number back to a decimal integer.
As an example of using Eq.(2), for the second stage (P = 2) of an N = 8-point DIT FFT, the k = 3 twiddle Q factor is:
k = 3 twiddle factor Q = [⌊3•22/8⌋]bit-rev
= [⌊1.5⌋]bit-rev = [1]bit-rev = 2.
The above [1]bit-rev operation is: take the decimal number 1 and represent it with log2(N)–1 = 2 bits, i.e., as 012. Next, reverse those bits to a binary 102 and convert that binary number to our desired decimal result of 2.
A Little History of the FFT
The radix-2 FFT has a very interesting history. For example, one of the driving forces behind the development of the FFT was the United State's desire to detect nuclear explosions inside the Soviet Union in the early 1960s. Also, if it hadn't been for the influence of a patent attorney, the Cooley-Tukey radix-2 FFT algorithm might well have been known as the Sande-Tukey algorithm, named after Gordon Sande and John Tukey. (That's the same Gordon Sande that occasionally posts on the comp.dsp newsgroup.) For those and other interesting FFT historical facts, see the following web sites.
Cooley and Tukey, "On the Origin of the FFT Paper", http://www.garfield.library.upenn.edu/classics1993/A1993MJ84500001.pdf
Rockmore, "The FFT - An Algorithm the Whole Family Can Use", http://www.cs.dartmouth.edu/~rockmore/cse-fft.pdf
Cipra, "The FFT: Making Technology Fly", http://compmack.googlecode.com/svn/marcoshack/calc4/The_FFT_Making_Technology_Fly.pdf
Cooley, Lewis, and Welch, "Historical Notes on the Fast Fourier Transform", http://www.signallake.com/innovation/FFTHistoryJun67.pdf
- Comments
- Write a Comment Select to add a comment

I've read your question and I can only guess what it means. If you're asking "What is a twiddle factor?", the simple answer is, a twiddle factor is a complex number whose magnitude is one. As such, multiplying a complex number whose magnitude is M by a twiddle factor produces a new complex number whose magnitude is also M. But the new complex number has a new (changed) phase angle. The word "twiddle" is a rarely-used American expression (slang) meaning "to spin or rotate in a small way." For example, "He twiddled the cigar in his mouth."
[-Rick-]

I can make no sense out of your comment. If you repeat your comment using proper English grammar and proper English spelling (and be as clear and specific as you can be), I will do my best to reply to your comment.
[-Rick-]

It's been years since I wrote this material. I see that I used the word "unique" three times, but I don't recall why I wrote those words. Looking back on what I wrote I suggest that you merely ignore the words "unique." Sorry for any confusion.
[-Rick-]

Im not sure I understand your question. The algorithms for computing either the DIF or DIT twiddle factors do not depend on which X(m) output samples you want to compute. Knowing which X(m) output samples you want to compute determines which signal paths in Fig. 2 or Fig. 3 need to be implemented. By the way, if you only want to compute a single FFT output, X(5) for example, you should learn how to implement the Goertzel algorithm. Theres a lot of Goertzel algorithm information on the Internet.
[-Rick]

I don't understand your question. What "code of ifft" are you referring to? I've made no mention of 'inverse FFTs' in this blog. Perhaps you are confusing this blog of mine with some other blog.

in stage P = 1 the four twiddle factors are:
For k = 0, twiddle factor = 0
For k = 1, twiddle factor = 0
For k = 2, twiddle factor = 0
For k = 3, twiddle factor = 0.
In stage P = 2 the four twiddle factors are:
For k = 0, twiddle factor = 0
For k = 1, twiddle factor = 0
For k = 2, twiddle factor = 2
For k = 3, twiddle factor = 2.
In stage P = 3 the four twiddle factors are:
For k = 0, twiddle factor = 0
For k = 1, twiddle factor = 2
For k = 2, twiddle factor = 1
For k = 3, twiddle factor = 3.
I hope the above answers your question.
Hi, thanks for your very interesting article.
For a given N (number of samples) How many twiddle factors are needed to compute the radix-2 butterfly based FFT? Is N/2 the correct answer? That is, the number of butterflies at each stage.
Thanks,
Regards,
Samuel

Samuel, if you examine my Figure 2 and Figure 3 you'll see that for an N-point radix-2 FFT, there are log2(N) stages and each stage contains N/2 twiddle factors. So the answer to your question is: for an N-point radix-2 FFT, there are a total of (N/2)*log2(N) twiddle factors.
Thanks for quick answer!
I was wondering if some of the twiddle factors are actually repeated and do not need to be recomputed. How many factors do I actually need to keep in the memory?
Thank you,
Samuel

If you use MATLAB, have a look at my code at:
https://www.dsprelated.com/showcode/232.php
If you run that code, with N = 16, and then enter the command:
Twiddles = exp(j*2*pi*Results(:,3)/N)
you'll see that some twiddle factors differ by only by the sign of their real parts. [Such as a twiddle at +22.5 degrees (0.9239+0.3827i) and a twiddle at +157.5 degrees (-0.9239+0.3827i).] Perhaps you can think of a way to take advantage of that symmetry.
I get how to calculate the twiddle factor for Q in this article thats fine, but not how you link it all together for the fft.
Take pass 2 in figure 3 for DIT:
X(6) has X(6) - Q(2)X(4)
How do you figure out that it needs Q(2) and X(4) and the - 1 based on just the index of 6 and pass P = 2
I want to map each index of the samples to the other needed index and the signed twiddle factor. No one seems to explain this part of the FFT.

Hi DaveSC.
You wrote: "Take pass 2 in figure 3 for DIT:". Does "pass 2" mean "stage 2"?
You wrote: "X(6) has X(6) - Q(2)X(4)". Keeping in mind that X(6) and X(4) are FFT output samples, what does "X(6) has X(6) - Q(2)X(4)" mean? What does the word "has" mean? What is Q(2)?
You wrote: "How do you figure out that it needs Q(2) and X(4) and the - 1 based on just the index of 6 and pass P = 2". In that sentence, what does the word "it" mean?
You wrote: "I can't figure out the math to map it so I can pre compute it before running the fft." In that sentence, what does the first "it" mean? In that sentence, what does the second "it" mean? What does the word "map" mean?
I don't understand exactly what processing you desire to perform.
Postscript 30 minutes later: DaveSC, I just saw your most recent comment on the 'signal processing StackExchange'. You're welcome to ignore my above questions if you wish.
To post reply to a comment, click on the 'reply' button attached to each comment. To post a new comment (not a reply to a comment) check out the 'Write a Comment' tab at the top of the comments.
Please login (on the right) if you already have an account on this platform.
Otherwise, please use this form to register (free) an join one of the largest online community for Electrical/Embedded/DSP/FPGA/ML engineers:





















