5G NR QC-LDPC Encoding Algorithm

• Wireless

3GPP 5G has been focused on structured LDPC codes known as quasi-cyclic low-density parity-check (QC-LDPC) codes, which exhibit advantages over other types of LDPC codes with respect to the hardware implementations of encoding and decoding using simple shift registers and logic circuits.  

5G NR QC-LDPC  

Circulant Permutation Matrix

A circular permutation matrix ${\bf I}(P_{i,j})$ of size $Z_c \times Z_c$ is obtained by circularly shifting the identity matrix $\bf I$ of size $Z_c \times Z_c$ to the right $P_{i,j}$ times. We denoted this binary circulant permutation matrixas by $Q(P_{i,j})$, considering $Q(1)$ as an example,

$Q(1) = \begin{bmatrix} 0 & 1 & 0 & \ldots & 0\\ 0 & 0 & 1 & \ldots & 0\\ \vdots & \vdots & \ddots & \vdots \\0 & 0 & 0 & \ldots & 1\\1 & 0 & 0 & \ldots & 0\\ \end{bmatrix}$

For simple notation, $Q(−1)$ denotes the null matrix. 

All possible lifting sizes $Z_c$ are grouped into 8 sets, listed as $\text{follow}^{[1]}$:

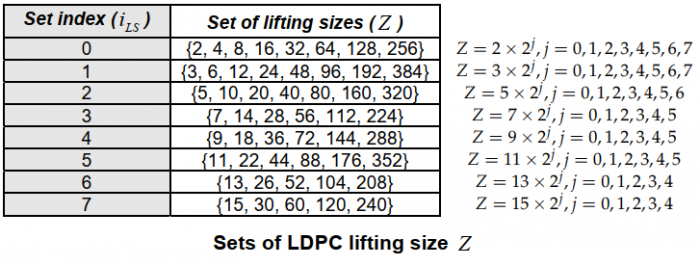
The parity-check matrix $\bf H$ of QC-LDPC code expressed by the following $m_b \times n_b$ array of $Z \times Z$ circulants over $GF(2)$:

$H = \begin{bmatrix}Q(P_{1,1}) & Q(P_{1,2}) & \ldots & Q(P_{1,n_b})\cr Q(P_{2,1}) & Q(P_{2,2}) & \ldots & Q(P_{2,n_b})\cr \vdots & \vdots & \ddots & \vdots \cr Q(P_{m_b,1}) & Q(P_{m_b,2}) & \ldots & Q(P_{m_b,n_b})\cr \end{bmatrix}$

Base Graphs Characteristics 

There are two rate-compatible base graphs with similar structures in 5G NR, denoted by BG1 and BG2.  

BG1 is targeted for larger block lengths and higher rates. BG2 is targeted for smaller block lengths and lower rates. If transport block size $A \le 292$, or if $A \le 3824$ and $R \le 2/3$ , or if $R \le 1/4$ , LDPC base graph 2 is used; otherwise, LDPC base graph 1 is used.

For BG1, a matrix of $H_{BG1}$ with a size of $m_b \times n_b(m_b = 46, n_b = 68, k_b = n_b - m_b = 22)$.  

For BG2, a matrix of $H_{BG2}$ with a size of $m_b \times n_b(m_b = 42, n_b = 52, k_b = n_b - m_b = 10)$.  

The information bit columns are $k_b \times Z$.  

The $H \in \{H_{BG1},H_{BG2}\}$ can be partitioned into six matrices:  

$H = \begin{bmatrix} A & B & 0\cr C_1 & C_2 & I\cr \end{bmatrix}$

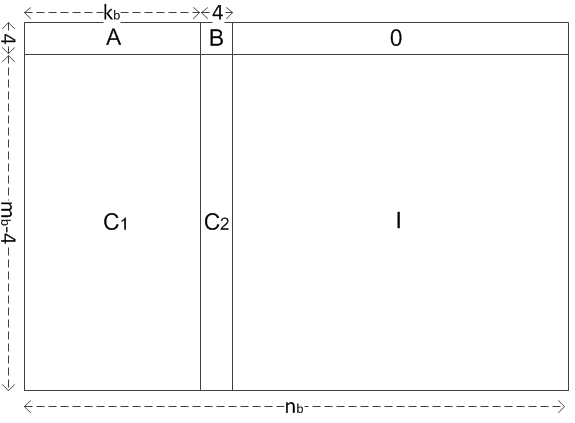
There are 8 different $i_{LS}$ for BG1 and 8 different $i_{LS}$ for BG2, that corresponding to 16 different $A, C_1, C_2$.  

$A = \begin{bmatrix}a_{1,1} & a_{1,2} & \ldots & a_{1,k_b}\cr a_{2,1} & a_{2,2} & \ldots & a_{2,k_b}\cr a_{3,1} & a_{3,2} & \ldots & a_{3,k_b}\cr a_{4,1} & a_{4,2} & \ldots & a_{4,k_b}\cr \end{bmatrix} C_1 = \begin{bmatrix} c_{1,1} & c_{1,2} & \ldots & c_{1,k_b}\cr c_{2,1} & c_{2,2} & \ldots & c_{2,k_b}\cr \vdots & \vdots & \ddots & \vdots \cr c_{m_b-4,1} & c_{m_b-4,2} & \ldots & c_{m_b-4,k_b}\cr \end{bmatrix} C_2 = \begin{bmatrix} c_{1,k_b+1} & c_{1,k_b+2} & c_{1,k_b+3} & c_{1,k_b+4}\cr c_{2,k_b+1} & c_{2,k_b+2} & c_{1,k_b+3} & c_{2,k_b+4}\cr \vdots & \vdots & \vdots & \vdots \cr c_{m_b-4,k_b+1} & c_{m_b-4,k_b+2} & c_{m_b-4,k_b+3} & c_{m_b-4,k_b+4}\cr \end{bmatrix}$

For simple notation, $\{-1, 0, 1, ...\}$ denotes the $\{Q(-1), Q(0), Q(1)...\}$.  

There are 2 types of $B \in \{H_{BG1\_B1}, H_{BG1\_B2}, H_{BG2\_B1}, H_{BG2\_B2}\}$ in both BG1 and BG2.  

$H_{BG1\_B1} = \begin{bmatrix} 1 &  0 & -1 & -1\cr 0 &  0 &  0 & -1\cr -1 & -1 &  0 &  0\cr 1 & -1 & -1 &  0\cr \end{bmatrix} ~~ H_{BG1\_B2} = \begin{bmatrix} 0 & 0 & -1 & -1\cr 105 & 0 & 0 & -1\cr -1 & -1 & 0 & 0\cr 0 & -1 & -1 & 0\cr \end{bmatrix}$

$H_{BG1\_B1}$ is for $Z$ set index $i_{LS} = (0, 1, 2, 3, 4, 5, 7)$, $H_{BG1\_B2}$ is for $i_{LS} = (6)$.  

$H_{BG2\_B1} = \begin{bmatrix} 0 & 0 & -1 & -1\cr -1 & 0 & 0 & -1\cr 1 & -1 & 0 & 0\cr 0 & -1 & -1 & 0\cr \end{bmatrix} ~~ H_{BG2\_B2} = \begin{bmatrix} 1 & 0 & -1 & -1\cr -1 & 0 & 0 & -1\cr 0 & -1 & 0 & 0\cr 1 & -1 & -1 & 0\cr \end{bmatrix}$

$H_{BG2\_B1}$ is for $Z$ set index $i_{LS} = (0, 1, 2, 4, 5, 6)$, $H_{BG2\_B2}$ is for $i_{LS} = (3, 7)$.  

Encoding Algorithm

Let the codeword  

$C = [s \; p_b \; p_c] = [s_1, s_2, \ldots, s_{k_b}, p_{b_1}, p_{b_2}, p_{b_3}, p_{b_4}, p_{c_1}, p_{c_2}, \ldots, p_{c_{m_b-4}}]$

where each element of $C$ is a vector of length $Z$.  

The encoding of LDPC codes is carried out as follow:  

$HC^T = \begin{bmatrix} A & B & 0\\ C_1 & C_2 & I\\ \end{bmatrix} \begin{bmatrix} s^T\\ p_b^T\\ p_c^T\\ \end{bmatrix} = 0^T$

that is,  

$\begin{align} A s^T + B p_b^T &= 0^T \tag{1} \\ C_1 s^T + C_2 p_b^T + p_c^T &= 0^T \tag{2} \end{align}$

Computation of $p_b$ 

First we determinate the $p_b$ part from equation (1):  

$\begin{align} H_{BG1\_B1} &: \begin{cases}  \sum\limits_{j=1}^{k_b}a_{1,j}s_j + p_{b_1}^{(1)} + p_{b_2} = 0\\ \sum\limits_{j=1}^{k_b}a_{2,j}s_j + p_{b_1} + p_{b_2} + p_{b_3} = 0\\ \sum\limits_{j=1}^{k_b}a_{3,j}s_j + p_{b_3} + p_{b_4} = 0 \\ \sum\limits_{j=1}^{k_b}a_{4,j}s_j + p_{b_1}^{(1)} + p_{b_4} = 0 \end{cases};~~~~~~ H_{BG1\_B2} : \begin{cases} \sum\limits_{j=1}^{k_b}a_{1,j}s_j + p_{b_1} + p_{b_2} = 0\\ \sum\limits_{j=1}^{k_b}a_{2,j}s_j + p_{b_1}^{(105~mod~Z)} + p_{b_2} + p_{b_3} = 0\\ \sum\limits_{j=1}^{k_b}a_{3,j}s_j + p_{b_3} + p_{b_4} = 0\\ \sum\limits_{j=1}^{k_b}a_{4,j}s_j + p_{b_1} + p_{b_4} = 0 \end{cases};\\ \\ H_{BG2\_B1} &: \begin{cases}  \sum\limits_{j=1}^{k_b}a_{1,j}s_j + p_{b_1} + p_{b_2} = 0\\ \sum\limits_{j=1}^{k_b}a_{2,j}s_j + p_{b_2} + p_{b_3} = 0\\ \sum\limits_{j=1}^{k_b}a_{3,j}s_j + p_{b_1}^{(1)} + p_{b_3} + p_{b_4} = 0\\ \sum\limits_{j=1}^{k_b}a_{4,j}s_j + p_{b_1} + p_{b_4} = 0 \end{cases};~~~~~~ H_{BG2\_B2} : \begin{cases} \sum\limits_{j=1}^{k_b}a_{1,j}s_j + p_{b_1}^{(1)} + p_{b_2} = 0\\ \sum\limits_{j=1}^{k_b}a_{2,j}s_j + p_{b_2} + p_{b_3} = 0\\ \sum\limits_{j=1}^{k_b}a_{3,j}s_j + p_{b_1} + p_{b_3} + p_{b_4} = 0\\\sum\limits_{j=1}^{k_b}a_{4,j}s_j + p_{b_1}^{(1)} + p_{b_4} = 0 \end{cases}.\end{align}$

where $p_{b_1}^{(\alpha)}$ denotes the $\alpha^{th}$ right cyclic shifted version of $p_{b_1}$ for $0 ≤ \alpha ≤ Z$.  

Based on the definition below,  

$\lambda_i = \sum\limits_{j=1}^{k_b}a_{i,j}s_j; ~~ i = 1, 2, 3, 4$.

the following can be obtained:  

$\begin{align}H_{BG1\_B1} &: \begin{cases}  p_{b_1} = \sum\limits_{i=1}^{4} \lambda_i\\ p_{b_2} = \lambda_1 + p_{b_1}^{(1)}\\p_{b_4} = \lambda_4 + p_{b_1}^{(1)}\\p_{b_3} = \lambda_3 + p_{b_4}\end{cases};~~~~~~H_{BG1\_B2} : \begin{cases}p_{b_1}^{(105~mod~Z)} = \sum\limits_{i=1}^{4} \lambda_i \to p_{b_1}\\p_{b_2} = \lambda_1 + p_{b_1}\\p_{b_4} = \lambda_4 + p_{b_1}\\p_{b_3} = \lambda_3 + p_{b_4}\end{cases};\\ \\H_{BG2\_B1} &: \begin{cases} p_{b_1}^{(1)} = \sum\limits_{i=1}^{4} \lambda_i \to p_{b_1}\\p_{b_2} = \lambda_1 + p_{b_1}\\p_{b_3} = \lambda_2 + p_{b_2}\\p_{b_4} = \lambda_4 + p_{b_1}\end{cases};~~~~~~H_{BG2\_B2} : \begin{cases}p_{b_1} = \sum\limits_{i=1}^{4} \lambda_i\\p_{b_2} = \lambda_1 + p_{b_1}^{(1)}\\p_{b_3} = \lambda_2 + p_{b_2}\\p_{b_4} = \lambda_3 + p_{b_1}^{(1)}\end{cases}.\end{align}$

Computation of $p_c$ 

Secondly, the $p_c$ can be easily determined based on equation (2):  

$p_{c_i} = \sum\limits_{j=1}^{k_b}c_{i,j}s_j + \sum\limits_{j=1}^4 c_{i,k_b+j}p_{b_j},~~i=1,2,\ldots, m_b-4$.

Systematic Bit Puncturing

5G NR directly delete the first $2 \times Z$ systematic bits. Here ignore the procedures of CRC, rate-matching, HARQ and so on which included in a complete channel coding link.  

Reference:  

1. 3GPP TS 38.212. NR; Multiplexing and channel coding. 3rd Generation Partnership Project. www.3gpp.org.  

2. Tram Thi Bao Nguyen, Tuy Nguyen Tan, Hanho Lee. Efficient QC-LDPC Encoder for 5G New Radio. www.mdpi.com.  

Sign in