Waveforms that are their own Fourier Transform

Mea Culpa 

There are many scary things about writing a technical book. Can I make the concepts clear? It is worth the effort? Will it sell? But all of these pale compared to the biggest fear: What if I'm just plain wrong? Not being able to help someone is one thing, but leading them astray is far worse.

My book on DSP has now been published for almost ten years. I've found lots of typos, a few misstatements, and many places where the explanations confuse even me. But I have been lucky; there are only a few places where I am simply mistaken. Here is one of the bigger ones. On page 216, Chapter 10, I write:

"Is there a waveform that is its own Fourier Transform? The answer is yes, and there is only one: the Gaussian."

It is true that the Fourier Transform of a Gaussian is also a Gaussian. However, is this really the only one? Not hardly.

Mea Culpa. I'm sorry. I bet your forgiveness.

Simple Examples 

For instance, the null function meets this criterion. That is, a time domain signal with a value of zero corresponds to a frequency domain with a value of zero. Here is another example that is not so trivial, the impulse train. This goes by other names as well, such a the dirac comb, the shah function, and the bed of nails. It consists of evenly spaced impulses (delta functions) from negative to positive infinity, in both the time and frequency domains. Here is a reference if you are interested:

http://en.wikipedia.org/wiki/Shah_function

30 Second Drill 

If this were the extent of my mistake I wouldn't feel so bad. But, in fact, there are an infinite number of waveforms that are their own Fourier Transform. And I can convince you of this in about 30 seconds. Start your stopwatch.

As you know, the Fourier Transform of a rectangular pulse is the sinc function.

Also, the Fourier Transform of the sinc function is a rectangular pulse.

Now, think what happens when we create a third waveform by adding these two time domain signals together. That is, we create a third waveform by adding a rectangular pulse to a sinc function. What is the Fourier Transform of this third waveform?

Addition in the time domain corresponds to addition in the frequency domain. Therefore, the Fourier Transform of a "rectangular pulse plus a sinc function" is a "sinc function plus a rectangular pulse." That is, this third waveform is its own Fourier Transform.

With a few restrictions, any waveform added to the Fourier transform of the waveform, will have this key property.

Stop you stopwatch.

An Example 

The table below shows an example of how this works. We start with nine random numbers contained in a(k), with k running from 0 to 8. Next we create b(k) from a(k), where b(k) has even symmetry. Specifically, b(k) is equal to a(k) for the first nine points. Afterward, b(k) = a(16-k). That is, b(9) = a(7), b(10) = a(6), etc.

Why do we need to make the signal have even symmetry? Our goal is to find waveforms that are their own Fourier Transform. However, we are restricting our search to waveforms that are entirely real, that is, the imaginary part is zero. Therefore, the Fourier Transform must also be entirely real, or it wouldn't meet our criterion. In turn, this requires that the time domain signal have even symmetry. In other words, if a time domain signal does not have even symmetry, its Fourier transform will have an imaginary part, and therefore does not belong to the class of signals we are looking for. Here are two links on these topics if you need a refresher:

http://www.dspguide.com/ch5/7.htm

http://www.dspguide.com/ch12/5.htm

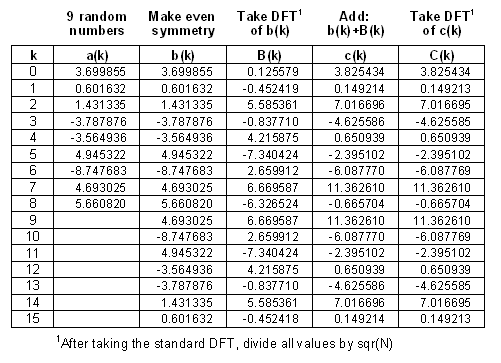
The next step is to take the DFT of b(k), which we will call, B(k). The simplest way is to run b(k) through a standard N=16 point DFT algorithm, such as the FFT. However, there is a subtle detail here. As you know, if you run a signal through the DFT, and then the Inverse DFT, you end up with what you started with. Somewhere along this path you encounter a 1/N scaling factor. This may be placed in the DFT, the Inverse DFT, or split between the two. Most algorithms, including the standard FFT, place this scaling factor on the DFT. However, for our method we need the factor split, with 1/SQR(N) placed with each. In short, we calculate B(k) by taking the conventional DFT of b(k), and then dividing all of the numbers by SQR(N).

Now things move quickly. We add b(k) to B(k) to form c(k), and then take the DFT of c(k) to find C(k).

Voila! We find that c(k) is identical to C(k), except for round-off error in the DFT. We have created a waveform that is its own Fourier Transform.

Is there a waveform that is its own Fourier Transform?

I said: Yes, and there is only one. The correct answer is: Yes, there are an infinite number. Do I get partial credit?  Say, 100% x 1/infinity?

Steve Smith

1/16/2008