A Simple Complex Down-conversion Scheme
It works like this: say we have a real xR(n) input bandpass signal having the spectrum shown in Figure 1(b), and for our example the sample rate is fs = 24 kHz. The Delay/Hilbert transform filter combination in Figure 1(a) attenuates the negative frequency spectral components of XR(f) to produce the complex uI(n) + juQ(n) signal whose spectrum is provided in Figure 1(c). (The first Delay function in the top path is a cascade of unit delay elements, whose length is the group delay of the Hilbert filter, needed to time-synchronize the uI(n) and uQ(n) sequences.) The follow-on downsample by four (discard all but every fourth sample) performs our desired frequency translation and produces the complex v(m) sequence having the spectrum shown in Figure 1(d) where the new sample rate is 6 kHz.
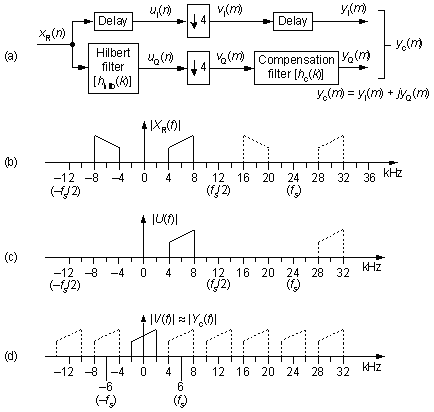
Figure 1
The compensation filter in Figure 1(a) is used to compensate for the non-flat frequency magnitude response of the Hilbert filter in order to widen the down-converter's usable passband width. (The Delay function after the downsampling in the top path is needed to time-synchronize the yI(m) and yQ(m) sequences.) To make this complex down-converter computationally efficient, I suggest the implementation shown in Figure 2, where the compensation filter's coefficients are hc(0) = -1/32, and hc(1) = 1/2 + 1/16.
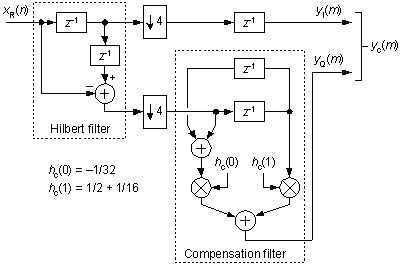
Figure 2
If the xR(n) input signal's bandwidth is no greater than fs/6, then Figure 2's Hilbert filter attenuates xR(n)'s undesired negative-frequency spectral components, at the yc(n) output, by approximately 35 dB. That much attenuation may not be something to write home about, but keep in mind that this down-converter requires no multipliers because the multiplies by the hc(0) and hc(1) coefficients can be implemented with binary shifts and adds. Now at the expensive of two multiplies per output sample, the compensation filter coefficients can be set to hc(0) = -0.02148 and hc(1) = 0.54128 to attenuate xR(n)'s undesired negative-frequency spectral components by roughly 45 dB.
Again, I thought some readers might find this little downconversion scheme to be interesting. If you have any questions, or comments, please let me know.
Copyright © 2008, Richard Lyons, All Rights Reserved
- Comments
- Write a Comment Select to add a comment

I am a bit delayed hehehe.
But, would you mind giving me the compensation filter for the scheme you have proposed above?
Thanks,
Aline

Hello ops_aline. To describe Figure 2's compensation filter in more detail; first, it's a tapped-delay line FIR filter having two delay elements and three coefficients. The delay line in Figure 2 is "folded" to reduce the number of necessary arithmetic operations per input sample. In its most efficient implementation the three coefficients are -1/32, 1/2+1/16, -1/32 allowing multiplication to be implemented with binary right shifts and additions. In this case the down-converter is multiplier-free.
For improved attenuation of the unwanted negative-frequency spectral components, the three coefficients can be -0.02148, 0.54128, -0.02148. (In which case the the down-converter is no longer multiplier-free.)

To post reply to a comment, click on the 'reply' button attached to each comment. To post a new comment (not a reply to a comment) check out the 'Write a Comment' tab at the top of the comments.
Please login (on the right) if you already have an account on this platform.
Otherwise, please use this form to register (free) an join one of the largest online community for Electrical/Embedded/DSP/FPGA/ML engineers:





















