Simultaneously Computing a Forward FFT and an Inverse FFT Using a Single FFT
Most of us are familiar with the processes of using a single N-point complex FFT to: (1) perform a 2N-point FFT on real data, and (2) perform two independent N-point FFTs on real data [1–5]. In case it's of interest to someone out there, this blog gives the algorithm for simultaneously computing a forward FFT and an inverse FFT using a single radix-2 FFT.
Our algorithm is depicted by the seven steps, S1 through S7, shown in Figure 1. In that figure, we compute the x(n) inverse FFT of the N-point frequency-domain conjugate symmetric input sequence X(m), as well as compute the Y(m) forward FFT of the N-point time-domain real-valued input sequence y(n) using the single complex FFT in step S4. Sample indices n and m both range from 0 to N–1 where N is an integer power of two.
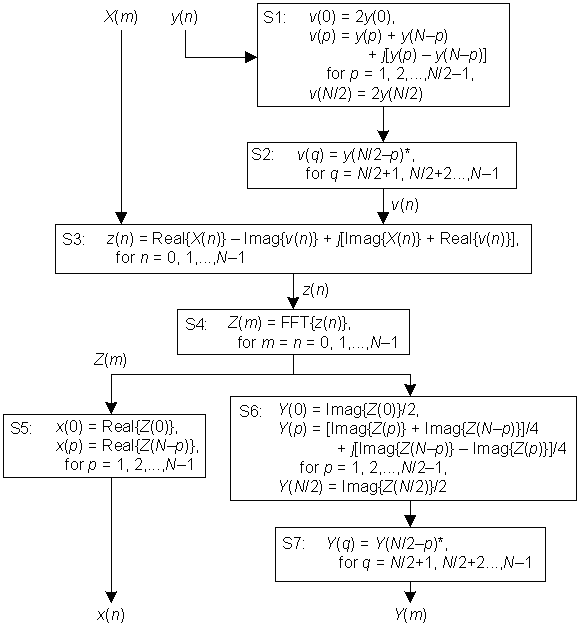
Figure 1.
At first glance Figure 1 looks more complicated than it actually is, and here's why:
- Steps S1 and S2 create a complex sequence that we call v(n).
- Step S1 generates the first N/2+1 samples of v(n) based on the real-valued input sequence y(n).
- Step S2 extends v(n) to a length of N samples and forces v(n) to be conjugate symmetric. The '*' symbol in step S2 means conjugation.
- Step S3 combines the conjugate symmetric sequences X(m) and v(n) to create a sequence we call z(n). (Sequence z(n) is not conjugate symmetric.)
- Step S4 is the algorithm's single radix-2 FFT operation, generating complex sequence Z(m).
- Step S5 generates the desired real-valued x(n) time sequence by performing a circular reversal of the real part of Z(m). (That is, other than the first sample, the real part of Z(m) samples are reversed in order to produce x(n).)
- Steps S6 and S7 generate the desired frequency-domain Y(m) sequence.
- Step S6 generates the first N/2+1 samples of Y(m).
- Step S7 extends the sequence from step S6 to a length of N samples, and forces conjugate symmetry, to produce Y(m). The '*' symbol in step S7 means conjugation.
I didn't invent this algorithm. Figure 1 is my interpretation and implementation of the discussion in Reference [6]. The Figure 1 algorithm's computational workload is one complex N-point FFT and roughly 2N additions/subtractions.
Below is a bit of MATLAB code demonstrating the process in Figure 1.
clear all, clc
% Create test input vectors
True_x = [1, 2, 3, 4, 5, 6, 7, 8]
X = fft(True_x);
y = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8];
True_Y = fft(y)
N = length(X);
% Create vector "v"
v(1) = 2*y(1); % Zero Hz sample
for p = 2:N/2 % Create 1st half of vector "v"
v(p) = y(p) + y(N-p+2) + j*(y(p) -y(N-p+2));
end
v(N/2+1) = 2*y(N/2+1); % Fs/2 sample
% Append conj. 2nd part of "v" vector
v(N/2+2:N) = fliplr(conj(v(2:N/2)));
% Create vector "z"
z = real(X) -imag(v) + j*(imag(X) + real(v));
% Perform single FFT
Z = fft(z);
% Create time-domain vector "x"
Real_Z = real(Z);
x = [Real_Z(1), fliplr(Real_Z(2:end))]/N
% Create freq-domain vector "Y"
Imag_Z = imag(Z);
Y(1) = Imag_Z(1)/2; % Zero Hz sample
for p = 2:N/2 % Create 1st half of vector "Y"
Y(p) = (Imag_Z(p) + Imag_Z(N-p+2) + ...
j*(Imag_Z(N-p+2) - Imag_Z(p)))/4;
end
Y(N/2+1) = Imag_Z(N/2+1)/2; % Fs/2 sample
% Append conj. 2nd part of "Y" vector
Y(N/2+2:N) = fliplr(conj(Y(2:N/2)))
% Stick a fork in me. I'm done.
References:
[1] Lyons, R. Understanding Digital Signal Processing, 2/E, Prentice Hall, Englewood Cliffs, New Jersey, 2004, pp. 488-500.
[2] Brigham, E. The fast Fourier Transform and Its Applications, Prentice Hall, Englewood Cliffs, New Jersey, 1988.
[3] Sorenson, H. et al., "Real Valued Fast Fourier Transform Algorithms," IEEE Trans. on Acoust. Speech, and Signal Proc., Vol. ASSP 35, No. 6, June 1987.
[4] Cooley, J. et al., "The Fast Fourier Transform Algorithm: Programming Considerations In the Calculation of Sine, Cosine and Laplace Transforms," Journal Sound Vib., Vol. 12, July 1970.
[5] Burrus, C. et al., Computer-Based Exercises for Signal Processing, Prentice Hall, Englewood Cliffs, New Jersey, 1994, pp. 53.
[6] Moshe, S. and Hertz, D. "On computing DFT of real N-point vector and IDFT of DFT-transformed real N-point vector via single DFT", Signal Processing Letters, IEEE, Volume: 6, Issue: 6, June 1999, p. 141.
- Comments
- Write a Comment Select to add a comment


To post reply to a comment, click on the 'reply' button attached to each comment. To post a new comment (not a reply to a comment) check out the 'Write a Comment' tab at the top of the comments.
Please login (on the right) if you already have an account on this platform.
Otherwise, please use this form to register (free) an join one of the largest online community for Electrical/Embedded/DSP/FPGA/ML engineers:





















