Python zplane function
Python is a popular general purpose programming language with powerful numerical and scientific packages, numpy and scipy. The Python ecosystem also has a impressive plotting package, matplotlib. The language and packages (the Python ecosystem) creates an ideal computing platform for Science and Engineering analysis and design.
But the current distributions does not include a zplane function which many DSP'ers might use because it is availabe in other packages Matlab, Octave, etc. Below is a function to implement similar behavior to the common used zplane function.
The zplane function takes the numerator and denominator polynomial representation of a transfer function and plots the complex z-plane poles and zeros.
For those unfamiliar with a numerical computing package, polynomials are usually represented least order coefficient to the highest order coefficient. An array assignment might look like the following, where *N* is the polynomial order.
The function below will plot a complex zplane given an array of b and a coefficients, numerator and denominator respectively.
This code requires the following packages:
- matplotlib (plotting routines)
- numpy (array object and roots)
Example usage:
>>> import numpy as np
# If the code is in a file called plot_zplane.py
>>> from plot_zplane import zplane
>>> b = np.array([0, 1, 1])
>>> a = np.array([1, 1/4., -3/8.])
>>> zplane(b,a)
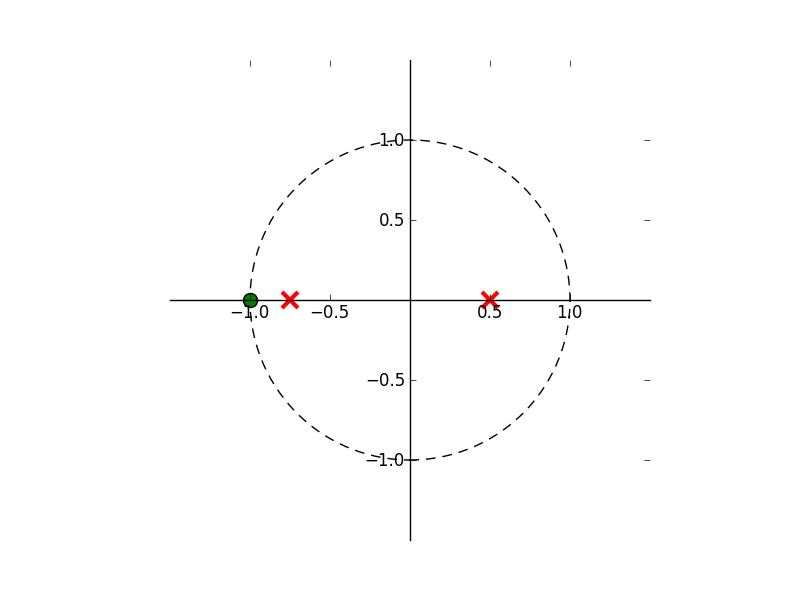
#
# Copyright (c) 2011 Christopher Felton
#
# This program is free software: you can redistribute it and/or modify
# it under the terms of the GNU Lesser General Public License as published by
# the Free Software Foundation, either version 3 of the License, or
# (at your option) any later version.
#
# This program is distributed in the hope that it will be useful,
# but WITHOUT ANY WARRANTY; without even the implied warranty of
# MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
# GNU Lesser General Public License for more details.
#
# You should have received a copy of the GNU Lesser General Public License
# along with this program. If not, see <http://www.gnu.org/licenses/>.
#
# The following is derived from the slides presented by
# Alexander Kain for CS506/606 "Special Topics: Speech Signal Processing"
# CSLU / OHSU, Spring Term 2011.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import patches
from matplotlib.figure import Figure
from matplotlib import rcParams
def zplane(b,a,filename=None):
"""Plot the complex z-plane given a transfer function.
"""
# get a figure/plot
ax = plt.subplot(111)
# create the unit circle
uc = patches.Circle((0,0), radius=1, fill=False,
color='black', ls='dashed')
ax.add_patch(uc)
# The coefficients are less than 1, normalize the coeficients
if np.max(b) > 1:
kn = np.max(b)
b = b/float(kn)
else:
kn = 1
if np.max(a) > 1:
kd = np.max(a)
a = a/float(kd)
else:
kd = 1
# Get the poles and zeros
p = np.roots(a)
z = np.roots(b)
k = kn/float(kd)
# Plot the zeros and set marker properties
t1 = plt.plot(z.real, z.imag, 'go', ms=10)
plt.setp( t1, markersize=10.0, markeredgewidth=1.0,
markeredgecolor='k', markerfacecolor='g')
# Plot the poles and set marker properties
t2 = plt.plot(p.real, p.imag, 'rx', ms=10)
plt.setp( t2, markersize=12.0, markeredgewidth=3.0,
markeredgecolor='r', markerfacecolor='r')
ax.spines['left'].set_position('center')
ax.spines['bottom'].set_position('center')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# set the ticks
r = 1.5; plt.axis('scaled'); plt.axis([-r, r, -r, r])
ticks = [-1, -.5, .5, 1]; plt.xticks(ticks); plt.yticks(ticks)
if filename is None:
plt.show()
else:
plt.savefig(filename)
return z, p, k

















