Allpass Problems
- The BiQuad Allpass Section
- Show that every second-order filter having transfer function
is a unit-gain allpass filter. That is, show that
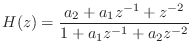
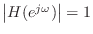 ,
for all
,
for all  and
and 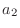 . (Typically,
. (Typically,  and
and 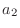 are chosen such
that the filter is stable, but this is not necessary for the result to hold.)
are chosen such
that the filter is stable, but this is not necessary for the result to hold.)
- Find the zeros of the filter as a function of the poles.
In other words, given two poles, what is the rule for placing the zeros
in order to obtain an allpass filter?
- Find the phase response of the zeros in terms of the phase response of the poles.
- Show that every second-order filter having transfer function
Next Section:
Existence of the Laplace Transform
Previous Section:
Multi-Input, Multi-Output (MIMO) Allpass Filters




















