Alternate Stability Criterion
In §5.6 (page ![]() ), a filter was defined to
be stable if its impulse response
), a filter was defined to
be stable if its impulse response ![]() decays to 0 in
magnitude as time
decays to 0 in
magnitude as time ![]() goes to infinity. In §6.8.5, we saw that
the impulse response of every finite-order LTI filter can be expressed
as a possible FIR part (which is always stable) plus a linear
combination of terms of the form
goes to infinity. In §6.8.5, we saw that
the impulse response of every finite-order LTI filter can be expressed
as a possible FIR part (which is always stable) plus a linear
combination of terms of the form
![]() , where
, where ![]() is some
finite-order polynomial in
is some
finite-order polynomial in ![]() , and
, and ![]() is the
is the ![]() th pole of the
filter. In this form, it is clear that the impulse response always
decays to zero when each pole is strictly inside the unit circle of
the
th pole of the
filter. In this form, it is clear that the impulse response always
decays to zero when each pole is strictly inside the unit circle of
the ![]() plane, i.e., when
plane, i.e., when ![]() . Thus, having all poles strictly
inside the unit circle is a sufficient criterion for filter
stability. If the filter is observable (meaning that there are
no pole-zero cancellations in the transfer function from input to
output), then this is also a necessary criterion.
. Thus, having all poles strictly
inside the unit circle is a sufficient criterion for filter
stability. If the filter is observable (meaning that there are
no pole-zero cancellations in the transfer function from input to
output), then this is also a necessary criterion.
A transfer function with no pole-zero cancellations is said to be
irreducible. For example,
![]() is
irreducible, while
is
irreducible, while
![]() is reducible, since
there is the common factor of
is reducible, since
there is the common factor of
![]() in the numerator and
denominator. Using this terminology, we may state the following
stability criterion:
in the numerator and
denominator. Using this terminology, we may state the following
stability criterion:
This characterization of stability is pursued further in §8.4, and yet another stability test (most often used in practice) is given in §8.4.1.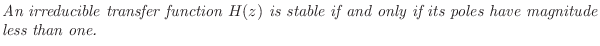
Next Section:
Summary of the Partial Fraction Expansion
Previous Section:
Repeated Poles



















