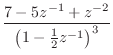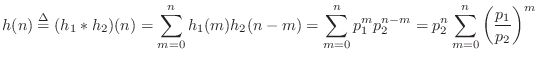Free Books
   Free Books    Introduction to Digital Filters  

Repeated Poles

When poles are repeated, an interesting new phenomenon emerges. To see what's going on, let's consider two identical poles arranged in parallel and in series. In the parallel case, we have

$\displaystyle H_1(z) \eqsp \frac{r_1}{1-pz^{-1}} + \frac{r_2}{1-pz^{-1}} \eqsp \frac{r_1+r_2}{1-pz^{-1}} \isdefs \frac{r_3}{1-pz^{-1}}. $

In the series case, we get

$\displaystyle H_2(z) \eqsp \frac{r_1}{1-pz^{-1}} \cdot \frac{r_2}{1-pz^{-1}} \eqsp \frac{r_1r_2}{(1-pz^{-1})^2} \isdefs \frac{r_3}{(1-pz^{-1})^2}. $

Thus, two one-pole filters in parallel are equivalent to a new one-pole filter7.8 (when the poles are identical), while the same two filters in series give a two-pole filter with a repeated pole. To accommodate both possibilities, the general partial fraction expansion must include the terms

$\displaystyle \frac{r_{1,1}}{(1-pz^{-1})^2} + \frac{r_{1,2}}{(1-pz^{-1})} $

for a pole $ p$ having multiplicity 2.

Dealing with Repeated Poles Analytically

A pole of multiplicity $ m_i$ has $ m_i$ residues associated with it. For example,

$\displaystyle H(z)$ $\displaystyle \isdef$ $\displaystyle \frac{7 - 5z^{-1}+ z^{-2}}{\left(1-\frac{1}{2}z^{-1}\right)^3}$  
  $\displaystyle =$ $\displaystyle \frac{1}{\left(1-\frac{1}{2}z^{-1}\right)^3} + \frac{2}{\left(1-\frac{1}{2}z^{-1}\right)^2} + \frac{4}{\left(1-\frac{1}{2}z^{-1}\right)} \protect$ (7.12)

and the three residues associated with the pole $ z=1/2$ are 1, 2, and 4.

Let $ r_{ij}$ denote the $ j$th residue associated with the pole $ p_i$, $ j=1,\ldots,m_i$. Successively differentiating $ (1-p_iz^{-1})^{m_i}H(z)$ $ k-1$ times with respect to $ z^{-1}$ and setting $ z=p_i$ isolates the residue $ r_{ik}$:

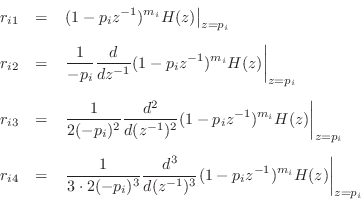
\begin{eqnarray*} r_{i1} &=& \left.(1-p_iz^{-1})^{m_i}H(z)\right\vert _{z=p_i}\\... ...ac{d^3}{d(z^{-1})^3} (1-p_iz^{-1})^{m_i}H(z)\right\vert _{z=p_i} \end{eqnarray*}

or

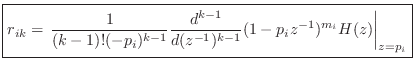
$\displaystyle \zbox {r_{ik} = \left.\frac{1}{(k-1)!(-p_i)^{k-1}}\frac{d^{k-1}}{d(z^{-1})^{k-1}} (1-p_iz^{-1})^{m_i}H(z)\right\vert _{z=p_i}} $

Example

For the example of Eq.$ \,$(6.12), we obtain

\begin{eqnarray*} r_{11} &=& \left.\left(1-\frac{1}{2}z^{-1}\right)^3H(z)\right\... ...}{dz^{-1}} (-5 + 2z^{-1})\right\vert _{z^{-1}=2} = 2\cdot 2 = 4. \end{eqnarray*}

Impulse Response of Repeated Poles

In the time domain, repeated poles give rise to polynomial amplitude envelopes on the decaying exponentials corresponding to the (stable) poles. For example, in the case of a single pole repeated twice, we have

$\displaystyle \zbox {\frac{1}{\left(1-pz^{-1}\right)^2} \;\longleftrightarrow\; (n+1) p^n, \quad n=0,1,2,\ldots\,.} $


Proof: First note that

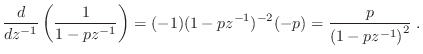
$\displaystyle \frac{d}{dz^{-1}}\left(\frac{1}{1-pz^{-1}}\right) = (-1)(1-pz^{-1})^{-2}(-p) = \frac{p}{\left(1-pz^{-1}\right)^2}\;. $

Therefore,
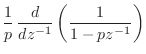$\displaystyle \frac{1}{\left(1-pz^{-1}\right)^2}$ $\displaystyle =$ $\displaystyle \frac{1}{p}\, \frac{d}{dz^{-1}}\left(\frac{1}{1-pz^{-1}}\right)$  
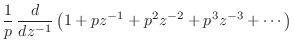  $\displaystyle =$ $\displaystyle \frac{1}{p}\, \frac{d}{dz^{-1}} \left(1 + pz^{-1}+ p^2z^{-2}+ p^3 z^{-3} + \cdots \right)$  
  $\displaystyle =$ $\displaystyle \frac{1}{p} \left(0 + p + 2p^2z^{-1}+ 3p^3z^{-2}+ \cdots \right)$  
  $\displaystyle =$ $\displaystyle 1 + 2pz^{-1}+ 3p^2z^{-2}+ \cdots$  
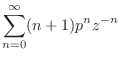  $\displaystyle =$ $\displaystyle \sum_{n=0}^{\infty}(n+1)p^n z^{-n}$  
  $\displaystyle \isdef$ $\displaystyle {\cal Z}\left\{(n+1)p^n\right\} \;\longleftrightarrow\; (n+1)p^n.$ (7.13)

Note that $ n+1$ is a first-order polynomial in $ n$. Similarly, a pole repeated three times corresponds to an impulse-response component that is an exponential decay multiplied by a quadratic polynomial in $ n$, and so on. As long as $ \vert p\vert<1$, the impulse response will eventually decay to zero, because exponential decay always overtakes polynomial growth in the limit as $ n$ goes to infinity.

So What's Up with Repeated Poles?

In the previous section, we found that repeated poles give rise to polynomial amplitude-envelopes multiplying the exponential decay due to the pole. On the other hand, two different poles can only yield a convolution (or sum) of two different exponential decays, with no polynomial envelope allowed. This is true no matter how closely the poles come together; the polynomial envelope can occur only when the poles merge exactly. This might violate one's intuitive expectation of a continuous change when passing from two closely spaced poles to a repeated pole.

To study this phenomenon further, consider the convolution of two one-pole impulse-responses $ h_1(n) = p_1^n$ and $ h_2(n) = p_2^n$:

$\displaystyle h(n) \isdef (h_1\ast h_2)(n) = \sum_{m=0}^n h_1(m)h_2(n-m) = \sum... ...^n p_1^{m}p_2^{n-m} = p_2^n\sum_{m=0}^n \left(\frac{p_1}{p_2}\right)^m \protect$ (7.14)

The finite limits on the summation result from the fact that both $ h_1$ and $ h_2$ are causal. Recall the closed-form sum of a truncated geometric series:

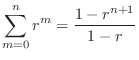
$\displaystyle \sum_{m=0}^n r^m = \frac{1-r^{n+1}}{1-r} $

Applying this to Eq.$ \,$(6.14) yields

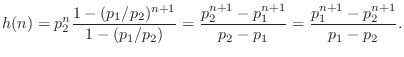
$\displaystyle h(n) = p_2^n \frac{1-(p_1/p_2)^{n+1}}{1-(p_1/p_2)} = \frac{p_2^{n+1}-p_1^{n+1}}{p_2-p_1} = \frac{p_1^{n+1}-p_2^{n+1}}{p_1-p_2}. $

Note that the result is symmetric in $ p_1$ and $ p_2$. If $ \left\vert p_1\right\vert>\left\vert p_2\right\vert$, then $ h(n)$ becomes proportional to $ p_1^n$ for large $ n$, while if $ \left\vert p_2\right\vert>\left\vert p_1\right\vert$, it becomes instead proportional to $ p_2^n$.

Going back to Eq.$ \,$(6.14), we have

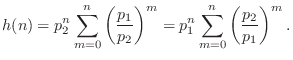$\displaystyle h(n) = p_2^n\sum_{m=0}^n \left(\frac{p_1}{p_2}\right)^m = p_1^n\sum_{m=0}^n \left(\frac{p_2}{p_1}\right)^m.$ (7.15)

Setting $ p_1=p_2=p$ yields

$\displaystyle h(n) = (n+1)p^n$ (7.16)

which is the first-order polynomial amplitude-envelope case for a repeated pole. We can see that the transition from ``two convolved exponentials'' to ``single exponential with a polynomial amplitude envelope'' is perfectly continuous, as we would expect.

We also see that the polynomial amplitude-envelopes fundamentally arise from iterated convolutions. This corresponds to the repeated poles being arranged in series, rather than in parallel. The simplest case is when the repeated pole is at $ p=1$, in which case its impulse response is a constant:

$\displaystyle \frac{1}{1-z^{-1}} \eqsp 1 + z^{-1}+ z^{-2}+ \cdots \;\longleftrightarrow\; [1,1,1,\ldots] $

The convolution of a constant with itself is a ramp:

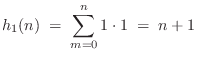
$\displaystyle h_1(n)\eqsp \sum_{m=0}^n 1\cdot 1 \eqsp n+1 $

The convolution of a constant and a ramp is a quadratic, and so on:7.9

\begin{eqnarray*} h_2(n)&=&\sum_{m=0}^n (m+1)\cdot 1 \eqsp \frac{(n+1)(n+2)}{2}\... ...+1)(m+2)}{2}\cdot 1\eqsp \frac{(n+1)(n+2)(n+3)}{3!}\\ &\cdots& \end{eqnarray*}

Next Section:
Alternate Stability Criterion
Previous Section:
Alternate PFE Methods