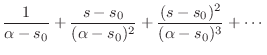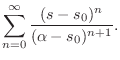Analytic Continuation
It turns out that the domain of definition of the Laplace transform can be extended
by means of analytic continuation [14, p. 259].
Analytic continuation is carried out by expanding a function of
![]() about all points in its domain of definition, and
extending the domain of definition to all points for which the series
expansion converges.
about all points in its domain of definition, and
extending the domain of definition to all points for which the series
expansion converges.
In the case of our exponential example
the Taylor series expansion of
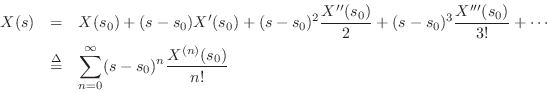
where, writing ![]() as
as
![]() and using the chain rule for
differentiation,
and using the chain rule for
differentiation,
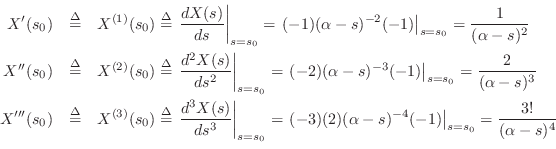
and so on. We also used the factorial notation
![]() , and we defined the special cases
, and we defined the special cases
![]() and
and
![]() , as is normally done.
The series expansion of
, as is normally done.
The series expansion of ![]() can thus be written
can thus be written
We now ask for what values of ![]() does the series Eq.
does the series Eq.![]() (D.2)
converge? The value
(D.2)
converge? The value ![]() is particularly easy to
check, since
is particularly easy to
check, since
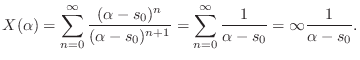
More generally, let's apply the ratio test for the convergence
of a geometric series. Since the ![]() th term of the series is
th term of the series is
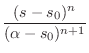
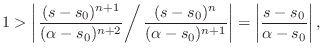
The analytic continuation of the domain of Eq.![]() (D.1) is now
defined as the union of the disks of convergence for all points
(D.1) is now
defined as the union of the disks of convergence for all points
![]() . It is easy to see that a sequence of such disks can
be chosen so as to define all points in the
. It is easy to see that a sequence of such disks can
be chosen so as to define all points in the ![]() plane except at the
pole
plane except at the
pole ![]() .
.
In summary, the Laplace transform of an exponential
![]() is
is
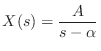
Analytic continuation works for any finite number of poles of finite order,D.2 and for an infinite number of distinct poles of finite order. It breaks down only in pathological situations such as when the Laplace transform is singular everywhere on some closed contour in the complex plane. Such pathologies do not arise in practice, so we need not be concerned about them.
Next Section:
Relation to the z Transform
Previous Section:
Existence of the Laplace Transform








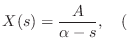 re
re