Free Books
   Free Books    Introduction to Digital Filters  

Constant Resonance Gain

It turns out it is possible to normalize exactly the resonance gain of the second-order resonator tuned by a single coefficient [89]. This is accomplished by placing the two zeros at $ z=\pm \sqrt{R}$, where $ R$ is the radius of the complex-conjugate pole pair . The transfer function numerator becomes $ B(z)=(1-\sqrt{R}z^{-1})(1+\sqrt{R}z^{-1}) = (1-Rz^{-2})$, yielding the total transfer function

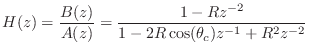
$\displaystyle H(z) = \frac{B(z)}{A(z)} = \frac{1 - Rz^{-2}}{1-2R\cos(\theta_c)z^{-1}+ R^2z^{-2}} $

which corresponds to the difference equation

$\displaystyle y(n) = x(n) - R\, x(n-2) + [2R\cos(\theta_c)] y(n-1) - R^2 y(n-2). $

We see there is one more multiply-add per sample (the term $ -R x(n-2)$) relative to the unnormalized two-pole resonator of Eq.$ \,$(B.13). The resonance gain is now

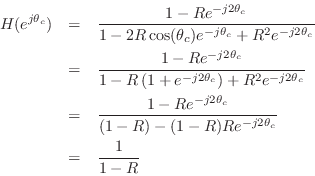
\begin{eqnarray*} H(e^{j\theta_c}) &=& \frac{1 - R e^{-j2\theta_c}}{1-2R\cos(\th... ...\theta_c}}{(1-R) - (1-R)Re^{-j2\theta_c}}\\ &=& \frac{1}{1 - R} \end{eqnarray*}

Thus, the gain at resonance is $ 1/(1-R)$ for all resonance tunings $ \theta _c$.

Figure B.19 shows a family of amplitude responses for the constant resonance-gain two-pole, for various values of $ \theta _c$ and $ R=0.99$. We see an excellent improvement in the regularity of the amplitude response as a function of tuning.

Figure: Frequency response overlays for the constant resonance-gain two-pole filter $ H(z)=(1-R)(1-Rz^{-2})/(1-2R\cos(\theta_c)z^{-1}+R^2z^{-2})$, for $ R=0.99$ and 10 values of $ \theta _c$ uniformly spaced from 0 to $ \pi $. The 5th case is plotted using thicker lines.
\includegraphics[width=\twidth ]{eps/cgresgain}

Next Section:
Peak Gain Versus Resonance Gain
Previous Section:
Normalizing Two-Pole Filter Gain at Resonance