First-Order
Parallel Sections
Figure 3.13 shows the impulse response of the real one-pole section
and Fig.
3.14 shows its
frequency response, computed using the
matlab utility
myfreqz listed in §
7.5.1. (Both
Matlab and Octave have compatible utilities
freqz, which
serve the same purpose.) Note that the
sampling rate is set to 1, and
the frequency axis goes from 0 Hz all the way to the
sampling rate,
which is appropriate for complex
filters (as we will soon see). Since
real filters have
Hermitian frequency responses (
i.e., an
even amplitude response and
odd phase response), they
may be plotted from 0 Hz to half the sampling rate without loss of
information.
Figure 3.13:
Impulse response of section 1 of
the example filter.
![\includegraphics[width=\twidth]{eps/arir1}](http://www.dsprelated.com/josimages_new/filters/img359.png) |
Figure 3.14:
Frequency response of section 1 of the example filter.
![\includegraphics[width=\twidth]{eps/arfr1}](http://www.dsprelated.com/josimages_new/filters/img360.png) |
Figure 3.15 shows the impulse response of the complex
one-pole section
and Fig.
3.16 shows the corresponding frequency response.
Figure 3.16:
Frequency response of complex
one-pole section 2.
![\includegraphics[width=\twidth]{eps/arcfr2}](http://www.dsprelated.com/josimages_new/filters/img363.png) |
The complex-conjugate section,
is of course quite similar, and is shown in Figures
3.17 and
3.18.
Figure 3.17:
Impulse response of complex
one-pole section 3 of the full partial-fraction-expansion of the
example filter.
![\includegraphics[width=\twidth]{eps/arcir3}](http://www.dsprelated.com/josimages_new/filters/img365.png) |
Figure 3.18:
Frequency response of complex
one-pole section 3.
![\includegraphics[width=\twidth]{eps/arcfr3}](http://www.dsprelated.com/josimages_new/filters/img366.png) |
Figure 3.19 shows the impulse response of the complex one-pole
section
and Fig.
3.20 shows its frequency response. Its complex-conjugate
counterpart,
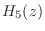
, is not shown since it is analogous to
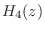
in relation to
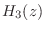
.
Figure 3.19:
Impulse response of complex
one-pole section 4 of the full partial-fraction-expansion of the
example filter.
![\includegraphics[width=\twidth]{eps/arcir4}](http://www.dsprelated.com/josimages_new/filters/img371.png) |
Figure 3.20:
Frequency response of complex
one-pole section 4.
![\includegraphics[width=\twidth]{eps/arcfr4}](http://www.dsprelated.com/josimages_new/filters/img372.png) |
Next Section: Parallel, Real, Second-Order SectionsPrevious Section: Sample-Level Implementation in Matlab
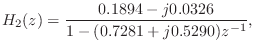
![\includegraphics[width=\twidth]{eps/arcir2}](http://www.dsprelated.com/josimages_new/filters/img362.png)
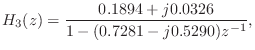
![\includegraphics[width=\twidth]{eps/arcir3}](http://www.dsprelated.com/josimages_new/filters/img365.png)
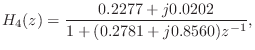
![\includegraphics[width=\twidth]{eps/arcir4}](http://www.dsprelated.com/josimages_new/filters/img371.png)








![\includegraphics[width=\twidth]{eps/arir1}](http://www.dsprelated.com/josimages_new/filters/img359.png)
![\includegraphics[width=\twidth]{eps/arfr1}](http://www.dsprelated.com/josimages_new/filters/img360.png)
![\includegraphics[width=\twidth]{eps/arcfr2}](http://www.dsprelated.com/josimages_new/filters/img363.png)
![\includegraphics[width=\twidth]{eps/arcfr3}](http://www.dsprelated.com/josimages_new/filters/img366.png)
![\includegraphics[width=\twidth]{eps/arcfr4}](http://www.dsprelated.com/josimages_new/filters/img372.png)











