Properties of Paraunitary Filter Banks
An ![]() -channel filter bank can be viewed as an
-channel filter bank can be viewed as an ![]() MIMO filter
MIMO filter
![$\displaystyle \mathbf{H}(z) = \left[\begin{array}{c} H_1(z) \\ [2pt] H_2(z) \\ [2pt] \vdots \\ [2pt] H_N(z)\end{array}\right]
$](http://www.dsprelated.com/josimages_new/filters/img1640.png)
A paraunitary filter bank must therefore obey
We can note the following properties of paraunitary filter banks:
- A synthesis filter bank
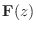 corresponding
to analysis filter bank
corresponding
to analysis filter bank
 is defined as that filter bank
which inverts the analysis filter bank, i.e., satisfies
Clearly, not every filter bank will be invertible in this way. When it is, it may be called a perfect reconstruction filter bank. When a filter bank transfer function
is defined as that filter bank
which inverts the analysis filter bank, i.e., satisfies
Clearly, not every filter bank will be invertible in this way. When it is, it may be called a perfect reconstruction filter bank. When a filter bank transfer function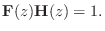
 is paraunitary, its
corresponding synthesis filter bank is simply the paraconjugate filter
bank
is paraunitary, its
corresponding synthesis filter bank is simply the paraconjugate filter
bank
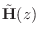 , or
, or

- The channel filters
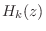 in a paraunitary filter bank
are power complementary:
This follows immediately from looking at the paraunitary property on the unit circle.
in a paraunitary filter bank
are power complementary:
This follows immediately from looking at the paraunitary property on the unit circle.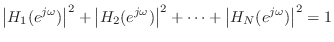
- When
 is FIR, the corresponding synthesis filter
matrix
is FIR, the corresponding synthesis filter
matrix
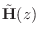 is also FIR. Note that this implies an FIR
filter-matrix can be inverted by another FIR filter-matrix. This is in
stark contrast to the case of single-input, single-output FIR filters,
which must be inverted by IIR filters, in general.
is also FIR. Note that this implies an FIR
filter-matrix can be inverted by another FIR filter-matrix. This is in
stark contrast to the case of single-input, single-output FIR filters,
which must be inverted by IIR filters, in general.
- When
 is FIR, each synthesis filter,
is FIR, each synthesis filter,
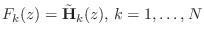 , is simply the
, is simply the 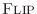 of its corresponding
analysis filter
of its corresponding
analysis filter
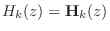 :
where
:
where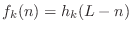
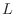 is the filter length. (When the filter coefficients are
complex,
is the filter length. (When the filter coefficients are
complex, 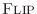 includes a complex conjugation as well.)
includes a complex conjugation as well.)
This follows from the fact that paraconjugating an FIR filter amounts to simply flipping (and conjugating) its coefficients.
Note that only trivial FIR filters can be paraunitary in the single-input, single-output (SISO) case. In the MIMO case, on the other hand, paraunitary systems can be composed of FIR filters of any order.
- FIR analysis and synthesis filters in paraunitary filter banks
have the same amplitude response.
This follows from the fact that
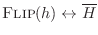 , i.e., flipping an FIR filter impulse response
, i.e., flipping an FIR filter impulse response  conjugates the frequency response, which does not affect its amplitude
response
conjugates the frequency response, which does not affect its amplitude
response
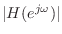 .
.
Next Section:
Mechanical Equivalent of a Capacitor is a Spring
Previous Section:
Properties of Paraunitary Systems



















