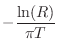Free Books
   Free Books    Introduction to Digital Filters  

Resonator Bandwidth in Terms of Pole Radius

The magnitude $ R$ of a complex pole determines the damping or bandwidth of the resonator. (Damping may be defined as the reciprocal of the bandwidth.)

As derived in §8.5, when $ R$ is close to 1, a reasonable definition of 3dB-bandwidth $ B$ is provided by

$\displaystyle B$ $\displaystyle \isdef$ $\displaystyle - \frac{\ln(R)}{\pi T}$ (B.4)
$\displaystyle R$ $\displaystyle =$ $\displaystyle e^{- \pi B T} \protect$ (B.5)

where $ R$ is the pole radius, $ B$ is the bandwidth in Hertz (cycles per second), and $ T$ is the sampling interval in seconds.

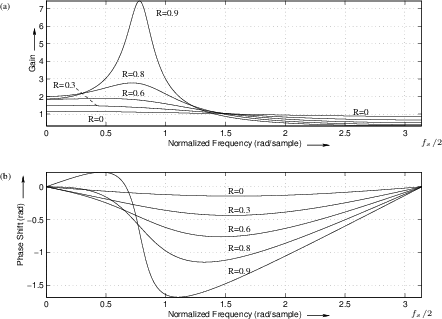
Figure B.6 shows a family of frequency responses for the two-pole resonator obtained by setting $ b_0 = 1$ and varying $ R$. The value of $ \theta _c$ in all cases is $ \pi /4$, corresponding to $ f_c = f_s/8$. The analytic expressions for amplitude and phase response are

\begin{eqnarray*} G(\omega)\! &=& \!\frac{b_0}{\sqrt{[1 + a_1 \cos(\omega T) + a... ... + a_1 \cos(\omega T) + a_2 \cos(2\omega T)}\right]\qquad(b_0>0) \end{eqnarray*}

where $ a_1 = - 2R \cos(\theta_c)$ and $ a_2 = R^2$.

Figure B.6: Frequency response of the two-pole filter
$ y(n) = x(n) + 2R \cos (\theta _c) y(n - 1) - R^2 y(n - 2)$
with $ \theta _c$ fixed at $ \pi /4$ and for various values of $ R$. (a) Amplitude response. (b) Phase response.
\begin{figure}\input fig/kfig2p23.pstex_t \end{figure}

Next Section:
Two-Pole Partial Fraction Expansion
Previous Section:
Trigonometric Identities, Continued