Two-Pole Partial Fraction Expansion

Free Books Introduction to Digital Filters

Note that every real two-pole resonator can be broken up into a sum of two complex one-pole resonators:

$\displaystyle H(z) = \frac{g}{(1 - p z^{-1}) (1 - \overline{p} z^{-1})} = \frac{g_1}{1-pz^{-1}} + \frac{g_2}{1-\overline{p}z^{-1}} \protect$

(B.7)

where

and

are constants (generally complex). In this ``parallel one-pole'' form, it can be seen that the peak gain is no longer equal to the resonance gain, since each one-pole frequency response is ``tilted'' near resonance by being summed with the ``skirt'' of the other one-pole resonator, as illustrated in Fig.B.9. This interaction between the positive- and negative-frequency poles is minimized by making the resonance sharper ( $\left\vert p\right\vert\to1$ ), and by separating the pole frequencies $0\ll\angle p \ll \pi$ . The greatest separation occurs when the resonance frequency is at one-fourth the sampling rate ( $\angle p =\pi/2$ ). However, low-frequency resonances, which are by far the most common in audio work, suffer from significant overlapping of the positive- and negative-frequency poles.

**Figure B.9:** Frequency response (solid lines) of the two-pole resonator

$H(z)=1/(1-2R\cos (\theta _c)z^{-1}+ R^2z^{-2})$ ,
for and $\theta _c = \pi /8$ , overlaid with the frequency responses (dashed lines) of its positive- and negative-frequency complex one-pole components. Also marked (dashed lines) are the two resonance frequencies; the peak frequencies can be seen to lie slightly outside the resonance frequencies.
$\includegraphics[width=\twidth ]{eps/tppfe}$

To show Eq. $\,$ (B.7) is always true, let's solve in general for and given and . Recombining the right-hand side over a common denominator and equating numerators gives

$\displaystyle g = g_1 - g_1 \overline{p}z^{-1}+ g_2 - g_2 pz^{-1}$

which implies

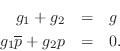
$\begin{eqnarray*} g_1+g_2 &=& g\\ g_1 \overline{p} + g_2 p &=& 0. \end{eqnarray*}$

The solution is easily found to be

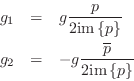
$\begin{eqnarray*} g_1 &=& g \frac{p}{2\mbox{im}\left\{p\right\}}\\ g_2 &=& -g \frac{\overline{p}}{2\mbox{im}\left\{p\right\}} \end{eqnarray*}$

where we have assumed im $\left\{p\right\}\neq 0$ , as necessary to have a resonator in the first place.

Breaking up the two-pole real resonator into a parallel sum of two complex one-pole resonators is a simple example of a partial fraction expansion (PFE) (discussed more fully in §6.8).

Note that the inverse z transform of a sum of one-pole transfer functions can be easily written down by inspection. In particular, the impulse response of the PFE of the two-pole resonator (see Eq. $\,$ (B.7)) is clearly

$\displaystyle h(n) = g_1 p^n + g_2 \overline{p}^n,\qquad n=0,1,2,\ldots$