DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  


Shift and Convolution Theorems

In this section, we prove the highly useful shift theorem and convolution theorem for unilateral z transforms. We consider the space of infinitely long, causal, complex sequences $ x(n)\in{\bf C}$, $ n\in{\bf Z}$, with $ x(n)=0$ for $ n < 0$.

Shift Theorem

The shift theorem says that a delay of $ \Delta$ samples in the time domain corresponds to a multiplication by $ z^{-\Delta}$ in the frequency domain:

$\displaystyle {\cal Z}_z\{$SHIFT$\displaystyle _\Delta\{x\}\} \;=\; z^{-\Delta} X(z), \; \Delta\ge 0, $

or, using more common notation,

$\displaystyle \zbox {x(n-\Delta) \;\leftrightarrow\; z^{-\Delta} X(z), \; \Delta\ge 0.} $

Thus, $ x(\cdot - \Delta)$, which is the waveform $ x(\cdot)$ delayed by $ \Delta$ samples, has the z transform $ z^{-\Delta}X(z)$.


Proof:

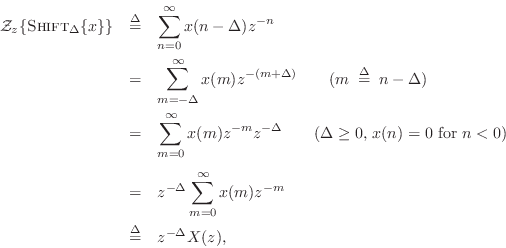
\begin{eqnarray*} {\cal Z}_z\{\mbox{{\sc Shift}}_\Delta\{x\}\} &\isdef & \sum_{n... ...ty}x(m) z^{-m} \\ &\isdef & z^{-\Delta} X(z), % \quad\pfendmath \end{eqnarray*}

where we used the causality assumption $ x(m)=0$ for $ m<0$.

Convolution Theorem

The convolution theorem for z transforms states that for any (real or) complex causal signals $ x$ and $ y$, convolution in the time domain is multiplication in the $ z$ domain, i.e.,

$\displaystyle \zbox {x\ast y \;\leftrightarrow\; X\cdot Y} $

or, using operator notation,

$\displaystyle {\cal Z}_z\{x \ast y\} \;=\; X(z)Y(z), $

where $ X(z)\isdef {\cal Z}_z(x)$, and $ Y(z)\isdef {\cal Z}_z(y)$. (See [84] for a development of the convolution theorem for discrete Fourier transforms.)


Proof:

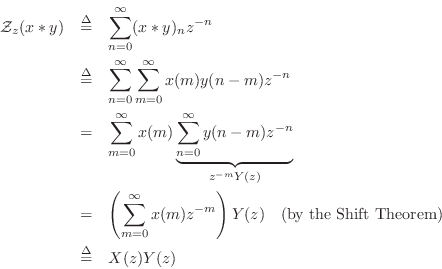
\begin{eqnarray*} {\cal Z}_z(x\ast y) &\isdef & \sum_{n=0}^{\infty}(x\ast y)_n z... ...(by the Shift Theorem)}\\ &\isdef & X(z)Y(z) % \quad\pfendmath \end{eqnarray*}

The convolution theorem provides a major cornerstone of linear systems theory. It implies, for example, that any stable causal LTI filter (recursive or nonrecursive) can be implemented by convolving the input signal with the impulse response of the filter, as shown in the next section.

Next Section:
Z Transform of Convolution
Previous Section:
Existence of the Z Transform