DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Z Transform of Convolution

From Eq.$ \,$(5.5), we have that the output $ y$ from a linear time-invariant filter with input $ x$ and impulse response $ h$ is given by the convolution of $ h$ and $ x$, i.e.,

$\displaystyle y(n) \eqsp (h \ast x)(n) \protect$ (7.3)

where ``$ \ast $'' means convolution as before. Taking the z transform of both sides of Eq.$ \,$(6.3) and applying the convolution theorem from the preceding section gives

$\displaystyle Y(z) \eqsp H(z)X(z) \protect$ (7.4)

where H(z) is the z transform of the filter impulse response. We may divide Eq.$ \,$(6.4) by $ X(z)$ to obtain

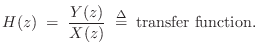
$\displaystyle H(z) \eqsp \frac{Y(z)}{X(z)} \;\isdef \; \hbox{transfer function}. $

This shows that, as a direct result of the convolution theorem, the z transform of an impulse response $ h(n)$ is equal to the transfer function $ H(z)=Y(z)/X(z)$ of the filter, provided the filter is linear and time invariant.

Next Section:
Z Transform of Difference Equations
Previous Section:
Shift and Convolution Theorems