Bessel Functions
The Bessel functions of the first kind may be defined as the
coefficients
![]() in the two-sided Laurent expansion
of the so-called
generating function
[84, p. 14],4.10
in the two-sided Laurent expansion
of the so-called
generating function
[84, p. 14],4.10
where
The last expression can be interpreted as the Fourier superposition of the sinusoidal harmonics of
Note that
![]() is real when
is real when ![]() is real. This can be seen
by viewing Eq.
is real. This can be seen
by viewing Eq.![]() (4.6) as the product of the series expansion for
(4.6) as the product of the series expansion for
![]() times that for
times that for
![]() (see footnote
pertaining to Eq.
(see footnote
pertaining to Eq.![]() (4.6)).
(4.6)).
Figure 4.15 illustrates the first eleven Bessel functions of the first
kind for arguments up to ![]() . It can be seen in the figure
that when the FM index
. It can be seen in the figure
that when the FM index ![]() is zero,
is zero, ![]() and
and ![]() for
all
for
all ![]() . Since
. Since
![]() is the amplitude of the carrier
frequency, there are no side bands when
is the amplitude of the carrier
frequency, there are no side bands when ![]() . As the FM index
increases, the sidebands begin to grow while the carrier term
diminishes. This is how FM synthesis produces an expanded, brighter
bandwidth as the FM index is increased.
. As the FM index
increases, the sidebands begin to grow while the carrier term
diminishes. This is how FM synthesis produces an expanded, brighter
bandwidth as the FM index is increased.
Next Section:
FM Spectra
Previous Section:
Example AM Spectra








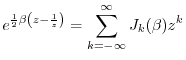
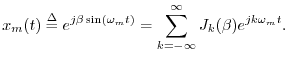
![\includegraphics[width=\twidth]{eps/bessel}](http://www.dsprelated.com/josimages_new/mdft/img537.png)











