Free Books    Mathematics of the DFT  

Downsampling Operator

Downsampling by $ L$ (also called decimation by $ L$) is defined for $ x\in{\bf C}^N$ as taking every $ L$th sample, starting with sample zero:

\begin{eqnarray*} \hbox{\sc Downsample}_{L,m}(x) &\isdef & x(mL),\\ m &=& 0,1,2,\ldots,M-1\\ N&=&LM. \end{eqnarray*}

The $ \hbox{\sc Downsample}_L()$ operator maps a length $ N=LM$ signal down to a length $ M$ signal. It is the inverse of the $ \hbox{\sc Stretch}_L()$ operator (but not vice versa), i.e.,

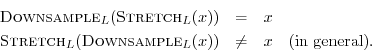
\begin{eqnarray*} \hbox{\sc Downsample}_L(\hbox{\sc Stretch}_L(x)) &=& x \\ \hb... ...L(\hbox{\sc Downsample}_L(x)) &\neq& x\quad \mbox{(in general).} \end{eqnarray*}

The stretch and downsampling operations do not commute because they are linear time-varying operators. They can be modeled using time-varying switches controlled by the sample index $ n$.

Figure: Illustration of $ \protect\hbox{\sc Downsample}_2(x)$.
\includegraphics[width=4in]{eps/downsamplex}

The following example of $ \protect\hbox{\sc Downsample}_2(x)$ is illustrated in Fig.7.10:

$\displaystyle \hbox{\sc Downsample}_2([0,1,2,3,4,5,6,7,8,9]) = [0,2,4,6,8]. $

Note that the term ``downsampling'' may also refer to the more elaborate process of sampling-rate conversion to a lower sampling rate, in which a signal's sampling rate is lowered by resampling using bandlimited interpolation. To distinguish these cases, we can call this bandlimited downsampling, because a lowpass-filter is needed, in general, prior to downsampling so that aliasing is avoided. This topic is address in Appendix D. Early sampling-rate converters were in fact implemented using the $ \hbox{\sc Stretch}_L$ operation, followed by an appropriate lowpass filter, followed by $ \hbox{\sc Downsample}_M$, in order to implement a sampling-rate conversion by the factor $ L/M$.

Next Section:
Alias Operator
Previous Section:
Repeat Operator