FFT of a Simple Sinusoid
Our first example is an FFT of the simple sinusoid
% Example 1: FFT of a DFT-sinusoid % Parameters: N = 64; % Must be a power of two T = 1; % Set sampling rate to 1 A = 1; % Sinusoidal amplitude phi = 0; % Sinusoidal phase f = 0.25; % Frequency (cycles/sample) n = [0:N-1]; % Discrete time axis x = A*cos(2*pi*n*f*T+phi); % Sampled sinusoid X = fft(x); % Spectrum % Plot time data: figure(1); subplot(3,1,1); plot(n,x,'*k'); ni = [0:.1:N-1]; % Interpolated time axis hold on; plot(ni,A*cos(2*pi*ni*f*T+phi),'-k'); grid off; title('Sinusoid at 1/4 the Sampling Rate'); xlabel('Time (samples)'); ylabel('Amplitude'); text(-8,1,'a)'); hold off; % Plot spectral magnitude: magX = abs(X); fn = [0:1/N:1-1/N]; % Normalized frequency axis subplot(3,1,2); stem(fn,magX,'ok'); grid on; xlabel('Normalized Frequency (cycles per sample))'); ylabel('Magnitude (Linear)'); text(-.11,40,'b)'); % Same thing on a dB scale: spec = 20*log10(magX); % Spectral magnitude in dB subplot(3,1,3); plot(fn,spec,'--ok'); grid on; axis([0 1 -350 50]); xlabel('Normalized Frequency (cycles per sample))'); ylabel('Magnitude (dB)'); text(-.11,50,'c)'); cmd = ['print -deps ', '../eps/example1.eps']; disp(cmd); eval(cmd);
![\includegraphics[width=\twidth]{eps/example1}](http://www.dsprelated.com/josimages_new/mdft/img1494.png) |
The results are shown in Fig.8.1. The time-domain signal is
shown in the upper plot (Fig.8.1a), both in pseudo-continuous
and sampled form. In the middle plot (Fig.8.1b), we see two
peaks in the magnitude spectrum, each at magnitude ![]() on a linear
scale, located at normalized frequencies
on a linear
scale, located at normalized frequencies ![]() and
and
![]() . A spectral peak amplitude of
. A spectral peak amplitude of
![]() is what we
expect, since
is what we
expect, since
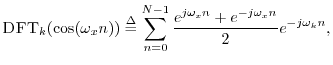
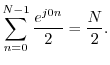
The spectrum should be exactly zero at the other bin numbers. How
accurately this happens can be seen by looking on a dB scale, as shown in
Fig.8.1c. We see that the spectral magnitude in the other bins is
on the order of ![]() dB lower, which is close enough to zero for audio
work
dB lower, which is close enough to zero for audio
work
![]() .
.
Next Section:
FFT of a Not-So-Simple Sinusoid
Previous Section:
Why a DFT is usually called an FFT in practice



















