The Inner Product

The inner product (or ``dot product'', or ``scalar product'') is an operation on two vectors which produces a scalar. Defining an inner product for a Banach space specializes it to a Hilbert space (or ``inner product space''). There are many examples of Hilbert spaces, but we will only need $\{{\bf C}^N,{\bf C}\}$ for this book (complex length vectors, and complex scalars).

The inner product between (complex) -vectors $\underline{u}$ and $\underline{v}$ is defined by^5.9

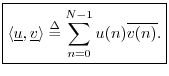
$\displaystyle \zbox {\left<\underline{u},\underline{v}\right> \isdef \sum_{n=0}^{N-1}u(n)\overline{v(n)}.}$

The complex conjugation of the second vector is done in order that a norm will be induced by the inner product:^5.10

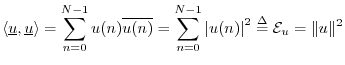
$\displaystyle \left<\underline{u},\underline{u}\right> = \sum_{n=0}^{N-1}u(n)\o... ...sum_{n=0}^{N-1}\left\vert u(n)\right\vert^2 \isdef {\cal E}_u = \Vert u\Vert^2$

As a result, the inner product is conjugate symmetric:

$\displaystyle \left<\underline{v},\underline{u}\right> = \overline{\left<\underline{u},\underline{v}\right>}$

Note that the inner product takes ${\bf C}^N\times{\bf C}^N$ to ${\bf C}$ . That is, two length complex vectors are mapped to a complex scalar.

Linearity of the Inner Product

Any function $f(\underline{u})$ of a vector $\underline{u}\in{\bf C}^N$ (which we may call an operator on ${\bf C}^N$ ) is said to be linear if for all $\underline{u}\in{\bf C}^N$ and $\underline{v}\in{\bf C}^N$ , and for all scalars $\alpha$ and $\beta$ in ${\bf C}$ ,

$\displaystyle f(\alpha \underline{u}+ \beta \underline{v}) = \alpha f(\underline{u}) + \beta f(\underline{v}).$

A linear operator thus ``commutes with mixing.'' Linearity consists of two component properties:

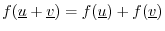
additivity: $f(\underline{u}+\underline{v}) = f(\underline{u}) + f(\underline{v})$
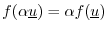
homogeneity: $f(\alpha \underline{u}) = \alpha f(\underline{u})$

A function of multiple vectors, e.g., $f(\underline{u},\underline{v},\underline{w})$ can be linear or not with respect to each of its arguments.

The inner product $\left<\underline{u},\underline{v}\right>$ is linear in its first argument, i.e., for all $\underline{u},\underline{v},\underline{w}\in{\bf C}^N$ , and for all $\alpha, \beta\in{\bf C}^N$ ,

$\displaystyle \left<\alpha \underline{u}+ \beta \underline{v},\underline{w}\rig... ...line{u},\underline{w}\right> + \beta \left<\underline{v},\underline{w}\right>.$

This is easy to show from the definition:

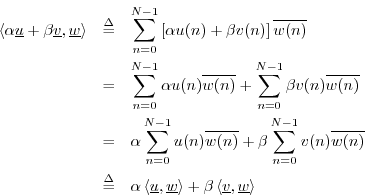
$\begin{eqnarray*} \left<\alpha \underline{u}+ \beta \underline{v},\underline{w}\... ...rline{w}\right> + \beta \left<\underline{v},\underline{w}\right> \end{eqnarray*}$

The inner product is also additive in its second argument, i.e.,

$\displaystyle \left<\underline{u},\underline{v}+ \underline{w}\right> = \left<\underline{u},\underline{v}\right> + \left<\underline{u},\underline{w}\right>,$

but it is only conjugate homogeneous (or antilinear) in its second argument, since

$\displaystyle \left<\underline{u},\alpha \underline{v}\right> = \overline{\alph... ...{u},\underline{v}\right> \neq \alpha \left<\underline{u},\underline{v}\right>.$

The inner product is strictly linear in its second argument with respect to real scalars and :

$\displaystyle \left<\underline{u},a \underline{v}+ b \underline{w}\right> = a \... ...ne{v}\right> + b \left<\underline{u},\underline{w}\right>, \quad a,b\in{\bf R}$

where $\underline{u},\underline{v},\underline{w}\in{\bf C}^N$ .

Since the inner product is linear in both of its arguments for real scalars, it may be called a bilinear operator in that context.

Norm Induced by the Inner Product

We may define a norm on $\underline{u}\in{\bf C}^N$ using the inner product:

$\displaystyle \zbox {\Vert\underline{u}\Vert \isdef \sqrt{\left<\underline{u},\underline{u}\right>}}$

It is straightforward to show that properties 1 and 3 of a norm hold (see §5.8.2). Property 2 follows easily from the Schwarz Inequality which is derived in the following subsection. Alternatively, we can simply observe that the inner product induces the well known

norm on ${\bf C}^N$ .

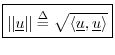
Cauchy-Schwarz Inequality

The Cauchy-Schwarz Inequality (or ``Schwarz Inequality'') states that for all $\underline{u}\in{\bf C}^N$ and $\underline{v}\in{\bf C}^N$ , we have

$\displaystyle \zbox {\left\vert\left<\underline{u},\underline{v}\right>\right\vert \leq \Vert\underline{u}\Vert\cdot\Vert\underline{v}\Vert}$

with equality if and only if $\underline{u}=c\underline{v}$ for some scalar

We can quickly show this for real vectors $\underline{u}\in{\bf R}^N$ , $\underline{v}\in{\bf R}^N$ , as follows: If either $\underline{u}$ or $\underline{v}$ is zero, the inequality holds (as equality). Assuming both are nonzero, let's scale them to unit-length by defining the normalized vectors $\underline{\tilde{u}}\isdeftext \underline{u}/\Vert\underline{u}\Vert$ , $\underline{\tilde{v}}\isdeftext \underline{v}/\Vert\underline{v}\Vert$ , which are unit-length vectors lying on the ``unit ball'' in ${\bf R}^N$ (a hypersphere of radius ). We have

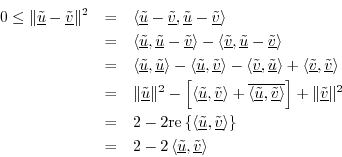
$\begin{eqnarray*} 0 \leq \Vert\underline{\tilde{u}}-\underline{\tilde{v}}\Vert^2... ...=& 2 - 2\left<\underline{\tilde{u}},\underline{\tilde{v}}\right> \end{eqnarray*}$

which implies

$\displaystyle \left<\underline{\tilde{u}},\underline{\tilde{v}}\right> \leq 1$

or, removing the normalization,

$\displaystyle \left<\underline{u},\underline{v}\right> \leq \Vert\underline{u}\Vert\cdot\Vert\underline{v}\Vert.$

The same derivation holds if $\underline{u}$ is replaced by $-\underline{u}$ yielding

$\displaystyle -\left<\underline{u},\underline{v}\right> \leq \Vert\underline{u}\Vert\cdot\Vert\underline{v}\Vert.$

The last two equations imply

$\displaystyle \left\vert\left<\underline{u},\underline{v}\right>\right\vert \leq \Vert\underline{u}\Vert\cdot\Vert\underline{v}\Vert.$

In the complex case, let $\left<\underline{u},\underline{v}\right>=R e^{j\theta}$ , and define $\underline{\tilde{v}}=\underline{v}e^{j\theta}$ . Then $\left<\underline{u},\underline{\tilde{v}}\right>$ is real and equal to $\vert\left<\underline{u},\underline{\tilde{v}}\right>\vert=R>0$ . By the same derivation as above,

$\displaystyle \left<\underline{u},\underline{\tilde{v}}\right>\leq\Vert\underli... ...derline{\tilde{v}}\Vert = \Vert\underline{u}\Vert\cdot\Vert\underline{v}\Vert.$

Since $\left<\underline{u},\underline{\tilde{v}}\right>=R=\left\vert\left<\underline{... ...right>\right\vert=\left\vert\left<\underline{u},\underline{v}\right>\right\vert$ , the result is established also in the complex case.

Triangle Inequality

The triangle inequality states that the length of any side of a triangle is less than or equal to the sum of the lengths of the other two sides, with equality occurring only when the triangle degenerates to a line. In ${\bf C}^N$ , this becomes

$\displaystyle \zbox {\Vert\underline{u}+\underline{v}\Vert \leq \Vert\underline{u}\Vert + \Vert\underline{v}\Vert.}$

We can show this quickly using the Schwarz Inequality:

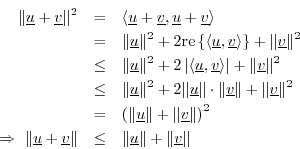
$\begin{eqnarray*} \Vert\underline{u}+\underline{v}\Vert^2 &=& \left<\underline{u... ...v}\Vert &\leq& \Vert\underline{u}\Vert + \Vert\underline{v}\Vert \end{eqnarray*}$

Triangle Difference Inequality

A useful variation on the triangle inequality is that the length of any side of a triangle is greater than the absolute difference of the lengths of the other two sides:

$\displaystyle \zbox {\Vert\underline{u}-\underline{v}\Vert \geq \left\vert\Vert\underline{u}\Vert - \Vert\underline{v}\Vert\right\vert}$

Proof: By the triangle inequality,

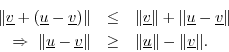
$\begin{eqnarray*} \Vert\underline{v}+ (\underline{u}-\underline{v})\Vert &\leq &... ...}\Vert &\geq& \Vert\underline{u}\Vert - \Vert\underline{v}\Vert. \end{eqnarray*}$

Interchanging $\underline{u}$ and $\underline{v}$ establishes the absolute value on the right-hand side.

Vector Cosine

The Cauchy-Schwarz Inequality can be written

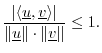
$\displaystyle \frac{\left\vert\left<\underline{u},\underline{v}\right>\right\vert}{\Vert\underline{u}\Vert\cdot\Vert\underline{v}\Vert} \leq 1.$

In the case of real vectors $\underline{u},\underline{v}$ , we can always find a real number $\theta\in[0,\pi]$ which satisfies

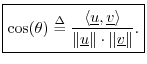
$\displaystyle \zbox {\cos(\theta) \isdef \frac{\left<\underline{u},\underline{v}\right>}{\Vert\underline{u}\Vert\cdot\Vert\underline{v}\Vert}.}$

We thus interpret $\theta$ as the angle between two vectors in ${\bf R}^N$ .

Orthogonality

The vectors (signals) and ^5.11are said to be orthogonal if $\left<x,y\right>=0$ , denoted $x\perp y$ . That is to say

$\displaystyle \zbox {x\perp y \Leftrightarrow \left<x,y\right>=0.}$

Note that if and are real and orthogonal, the cosine of the angle between them is zero. In plane geometry (), the angle between two perpendicular lines is $\pi/2$ , and $\cos(\pi/2)=0$ , as expected. More generally, orthogonality corresponds to the fact that two vectors in -space intersect at a right angle and are thus perpendicular geometrically.

Example ():

Let and , as shown in Fig.5.8.

**Figure 5.8:** Example of two orthogonal vectors for .
$\includegraphics[scale=0.7]{eps/ip}$

The inner product is $\left<x,y\right>=1\cdot \overline{1} + 1\cdot\overline{(-1)} = 0$ . This shows that the vectors are orthogonal. As marked in the figure, the lines intersect at a right angle and are therefore perpendicular.

The Pythagorean Theorem in N-Space

In 2D, the Pythagorean Theorem says that when and are orthogonal, as in Fig.5.8, (i.e., when the vectors and intersect at a right angle), then we have

$\displaystyle \Vert x+y\Vert^2 = \Vert x\Vert^2 + \Vert y\Vert^2$ $\displaystyle \mbox{($x\perp y$)}$ $\displaystyle . \protect$

(5.1)

This relationship generalizes to

dimensions, as we can easily show:

$\displaystyle \Vert x+y\Vert^2$	$\displaystyle =$	$\displaystyle \left<x+y,x+y\right>$
	$\displaystyle =$	$\displaystyle \left<x,x\right>+\left<x,y\right>+\left<y,x\right>+\left<y,y\right>$
	$\displaystyle =$	$\displaystyle \Vert x\Vert^2 + \left<x,y\right>+\overline{\left<x,y\right>} + \Vert y\Vert^2$
	$\displaystyle =$	$\displaystyle \Vert x\Vert^2 + \Vert y\Vert^2 + 2$ re $\displaystyle \left\{\left<x,y\right>\right\} \protect$	(5.2)

If $x\perp y$ , then $\left<x,y\right>=0$ and Eq. $\,$ (5.1) holds in

dimensions.

Note that the converse is not true in ${\bf C}^N$ . That is, $\Vert x+y\Vert^2 = \Vert x\Vert^2 + \Vert y\Vert^2$ does not imply $x\perp y$ in ${\bf C}^N$ . For a counterexample, consider , , in which case

$\displaystyle \Vert x+y\Vert^2 = \Vert 1+j,1-j\Vert^2 = 4 = \Vert x\Vert^2 + \Vert y\Vert^2$

while $\left<x,y\right> = j\cdot 1 + 1 \cdot\overline{-j} = 2j$ .

For real vectors $x,y\in{\bf R}^N$ , the Pythagorean theorem Eq. $\,$ (5.1) holds if and only if the vectors are orthogonal. To see this, note that, from Eq. $\,$ (5.2), when the Pythagorean theorem holds, either or is zero, or $\left<x,y\right>$ is zero or purely imaginary, by property 1 of norms (see §5.8.2). If the inner product cannot be imaginary, it must be zero.

Note that we also have an alternate version of the Pythagorean theorem:

$\displaystyle x\perp y\,\,\Rightarrow\,\, \Vert x-y\Vert^2 = \Vert x\Vert^2 + \Vert y\Vert^2$

Projection

The orthogonal projection (or simply ``projection'') of $y\in{\bf C}^N$ onto $x\in{\bf C}^N$ is defined by

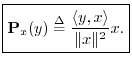
$\displaystyle \zbox {{\bf P}_{x}(y) \isdef \frac{\left<y,x\right>}{\Vert x\Vert^2} x.}$

The complex scalar $\left<y,x\right>/\Vert x\Vert^2$ is called the coefficient of projection. When projecting

onto a unit length vector

, the coefficient of projection is simply the inner product of

with

Motivation: The basic idea of orthogonal projection of onto is to ``drop a perpendicular'' from onto to define a new vector along which we call the ``projection'' of onto . This is illustrated for in Fig.5.9 for and , in which case

$\displaystyle {\bf P}_{x}(y) \isdef \frac{\left<y,x\right>}{\Vert x\Vert^2} x ... ...{1})}{4^2+1^2} x = \frac{11}{17} x= \left[\frac{44}{17},\frac{11}{17}\right].$

**Figure:** Projection of onto in 2D space.
$\includegraphics[scale=0.7]{eps/proj}$

Derivation: (1) Since any projection onto must lie along the line collinear with , write the projection as ${\bf P}_{x}(y)=\alpha x$ . (2) Since by definition the projection error $y-{\bf P}_{x}(y)$ is orthogonal to , we must have

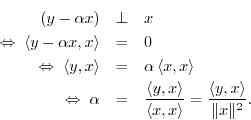
$\begin{eqnarray*} (y-\alpha x) & \perp & x\\ \;\Leftrightarrow\;\left<y-\alpha... ...}{\left<x,x\right>} = \frac{\left<y,x\right>}{\Vert x\Vert^2}. \end{eqnarray*}$

Thus,

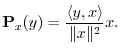
$\displaystyle {\bf P}_{x}(y) = \frac{\left<y,x\right>}{\Vert x\Vert^2} x.$

See §I.3.3 for illustration of orthogonal projection in matlab.

Next Section:
Signal Reconstruction from Projections
Previous Section:
Signal Metrics