Free Books
   Free Books    Mathematics of the DFT  

Plotting Complex Sinusoids versus Frequency

As discussed in the previous section, we regard the signal

$\displaystyle x(t) = A_x e^{j\omega_x t} $

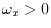
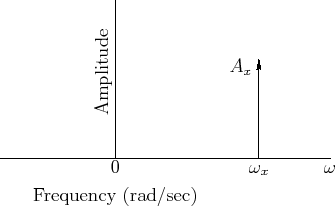
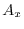
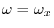
as a positive-frequency sinusoid when $ \omega_x>0$. In a manner analogous to spectral magnitude plots (discussed in §4.1.6), we can plot this complex sinusoid over a frequency axis as a vertical line of length $ A_x$ at the point $ \omega=\omega_x$, as shown in Fig.4.10. Such a plot of amplitude versus frequency may be called a spectral plot, or spectral representation [44] of the (zero-phase) complex sinusoid.

figure[htbp] \includegraphics{eps/csplot} More generally, however, a complex sinusoid has both an amplitude and a phase (or, equivalently, a complex amplitude):

$\displaystyle x(t) = \left(A_x e^{j\theta_x}\right)e^{j\omega_x t} $

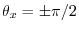
To accommodate the phase angle $ \theta_x$ in spectral plots, the plotted vector may be rotated by the angle $ \theta_x$ in the plane orthogonal to the frequency axis passing through $ \omega_x$, as done in Fig.4.16b below (p. [*]) for phase angles $ \theta_x=\pm \pi/2$.

Next Section:
Sinusoidal Amplitude Modulation (AM)
Previous Section:
Positive and Negative Frequencies