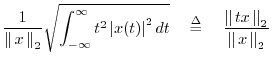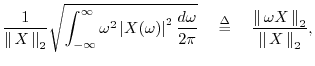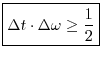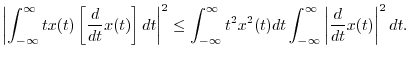Free Books
   Free Books    Mathematics of the DFT  

Selected Continuous-Time Fourier Theorems

This appendix presents Fourier theorems which are nice to know, but which do not, strictly speaking, pertain to the DFT. The differentiation theorem for Fourier Transforms comes up quite often, and its dual pertains as well to the DTFT (Appendix B). The scaling theorem provides an important basic insight into time-frequency duality. Finally, the very fundamental uncertainty principle is related to the scaling theorem.

Differentiation Theorem

Let $ x(t)$ denote a function differentiable for all $ t$ such that $ x(\pm\infty)=0$ and the Fourier Transforms (FT) of both $ x(t)$ and $ x^\prime(t)$ exist, where $ x^\prime(t)$ denotes the time derivative of $ x(t)$. Then we have

$\displaystyle \zbox {x^\prime(t) \;\longleftrightarrow\;j\omega X(\omega)} $

where $ X(\omega)$ denotes the Fourier transform of $ x(t)$. In operator notation:

$\displaystyle \zbox {\hbox{\sc FT}_{\omega}(x^\prime) = j\omega X(\omega)} $


Proof: This follows immediately from integration by parts:

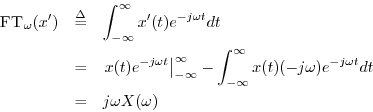
\begin{eqnarray*} \hbox{\sc FT}_{\omega}(x^\prime) &\isdef & \int_{-\infty}^\in... ...\infty x(t) (-j\omega)e^{-j\omega t} dt\\ &=& j\omega X(\omega) \end{eqnarray*}

since $ x(\pm\infty)=0$.

The differentiation theorem is implicitly used in §E.6 to show that audio signals are perceptually equivalent to bandlimited signals which are infinitely differentiable for all time.

Scaling Theorem

The scaling theorem (or similarity theorem) provides that if you horizontally ``stretch'' a signal by the factor $ \alpha$ in the time domain, you ``squeeze'' its Fourier transform by the same factor in the frequency domain. This is an important general Fourier duality relationship.


Theorem: For all continuous-time functions $ x(t)$ possessing a Fourier transform,

$\displaystyle \zbox {\hbox{\sc Scale}_\alpha(x) \;\longleftrightarrow\;\left\vert\alpha\right\vert\hbox{\sc Scale}_{(1/\alpha)}(X)} $

where

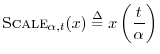
$\displaystyle \hbox{\sc Scale}_{\alpha,t}(x) \isdef x\left(\frac{t}{\alpha}\right) $

and $ \alpha$ is any nonzero real number (the abscissa stretch factor).


Proof: Taking the Fourier transform of the stretched signals gives

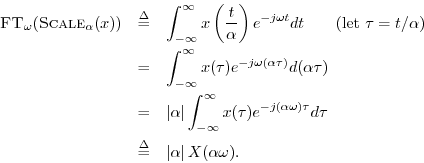
\begin{eqnarray*} \hbox{\sc FT}_{\omega}(\hbox{\sc Scale}_\alpha(x)) &\isdef & ... ...\tau \\ &\isdef & \left\vert\alpha\right\vert X(\alpha\omega). \end{eqnarray*}

The absolute value appears above because, when $ \alpha<0$, $ d (\alpha\tau) < 0$, which brings out a minus sign in front of the integral from $ -\infty$ to $ \infty$.

The scaling theorem is fundamentally restricted to the continuous-time, continuous-frequency (Fourier transform) case. The closest we came to the scaling theorem among the DFT theorems was the stretch theorem (§7.4.10). We found that ``stretching'' a discrete-time signal by the integer factor $ \alpha$ (filling in between samples with zeros) corresponded to the spectrum being repeated $ \alpha$ times around the unit circle. As a result, the ``baseband'' copy of the spectrum ``shrinks'' in width (relative to $ 2\pi $) by the factor $ \alpha$. Similarly, stretching a signal using interpolation (instead of zero-fill) corresponded to the same repeated spectrum with the spectral copies zeroed out. The spectrum of the interpolated signal can therefore be seen as having been stretched by the inverse of the time-domain stretch factor. In summary, the stretch theorem for DFTs can be viewed as the discrete-time, discrete-frequency counterpart of the scaling theorem for Fourier Transforms.

The Uncertainty Principle

The uncertainty principle (for Fourier transform pairs) follows immediately from the scaling theorem. It may be loosely stated as

Time Duration $ \times$ Frequency Bandwidth $ \geq$ c
where $ c$ is some constant determined by the precise definitions of ``duration'' in the time domain and ``bandwidth'' in the frequency domain.

If duration and bandwidth are defined as the ``nonzero interval,'' then we obtain $ c=\infty$, which is not very useful. This conclusion follows immediately from the definition of the Fourier transform and its inverse in §B.2.

Duration and Bandwidth as Second Moments

More interesting definitions of duration and bandwidth are obtained for nonzero signals using the normalized second moments of the squared magnitude:

$\displaystyle \Delta t$ $\displaystyle \isdef$ $\displaystyle \frac{1}{\left\Vert\,x\,\right\Vert _2} \sqrt{\int_{-\infty}^\inf... ...sdef \quad \frac{\left\Vert\,tx\,\right\Vert _2}{\left\Vert\,x\,\right\Vert _2}$  
$\displaystyle \Delta \omega$ $\displaystyle \isdef$ $\displaystyle \frac{1}{\left\Vert\,X\,\right\Vert _2} \sqrt{\int_{-\infty}^\inf... ...left\Vert\,\omega X\,\right\Vert _2}{\left\Vert\,X\,\right\Vert _2}, \protect$ (C.1)

    where

\begin{eqnarray*} \nonumber \\ [10pt] \left\Vert\,x\,\right\Vert _2^2 &\isdef &... ...}^\infty \left\vert X(\omega)\right\vert^2 \frac{d\omega}{2\pi}. \end{eqnarray*}

By the DTFT power theorem, which is proved in a manner analogous to the DFT case in §7.4.8, we have $ \left\Vert\,x\,\right\Vert _2=\left\Vert\,X\,\right\Vert _2$. Note that writing `` $ \left\Vert\,tx\,\right\Vert _2$'' and `` $ \left\Vert\,\omega X\,\right\Vert _2$'' is an abuse of notation, but a convenient one. These duration/bandwidth definitions are routinely used in physics, e.g., in connection with the Heisenberg uncertainty principle.C.1Under these definitions, we have the following theorem [52, p. 273-274]:


Theorem: If $ x(t) \ne 0$ and $ \sqrt{\vert t\vert}\,x(t) \to 0$ as $ \left\vert t\right\vert\to\infty$, then

$\displaystyle \zbox {\Delta t\cdot \Delta \omega \geq \frac{1}{2}} \protect$ (C.2)

with equality if and only if

$\displaystyle x(t) = Ae^{-\alpha t^2}, \quad \alpha>0, \quad A\ne 0. $

That is, only the Gaussian function (also known as the ``bell curve'' or ``normal curve'') achieves the lower bound on the time-bandwidth product.


Proof: Without loss of generality, we may take consider $ x(t)$ to be real and normalized to have unit $ L2$ norm ( $ \left\Vert\,x\,\right\Vert _2=1$). From the Schwarz inequality (see §5.9.3 for the discrete-time case),

$\displaystyle \left\vert\int_{-\infty}^\infty t x(t) \left[\frac{d}{dt}x(t)\rig... ...) dt \int_{-\infty}^\infty \left\vert\frac{d}{dt}x(t)\right\vert^2 dt. \protect$ (C.3)

The left-hand side can be evaluated using integration by parts:

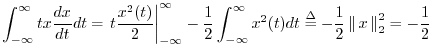
$\displaystyle \int_{-\infty}^\infty tx \frac{dx}{dt} dt = \left . t \frac{x^2(t... ...ty x^2(t) dt \isdef -\frac{1}{2}\left\Vert\,x\,\right\Vert _2^2 = -\frac{1}{2} $

where we used the assumption that $ \sqrt{\vert t\vert}\,x(t) \to 0$ as $ \left\vert t\right\vert\to\infty$.

The second term on the right-hand side of Eq.$ \,$(C.3) can be evaluated using the power theorem (§7.4.8 proves the discrete-time case) and differentiation theorem (§C.1 above):

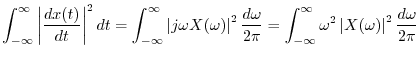
$\displaystyle \int_{-\infty}^\infty \left\vert\frac{dx(t)}{dt}\right\vert^2 dt ... ...\infty}^\infty \omega^2 \left\vert X(\omega)\right\vert^2 \frac{d\omega}{2\pi} $

Substituting these evaluations into Eq.$ \,$(C.3) gives

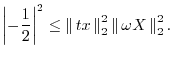
$\displaystyle \left\vert-\frac{1}{2}\right\vert^2 \leq \left\Vert\,tx\,\right\Vert _2^2 \left\Vert\,\omega X\,\right\Vert _2^2. $

Taking the square root of both sides gives the uncertainty relation sought.

If equality holds in the uncertainty relation Eq.$ \,$(C.2), then Eq.$ \,$(C.3) implies

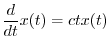
$\displaystyle \frac{d}{dt}x(t) = c t x(t) $

for some constant $ c$, which implies $ x(t)=A e^{\frac{c}{2} t^2}$ for some constants $ A$ and $ c$. Since $ x(\pm\infty)=0$ by hypothesis, we have $ c<0$ while $ A\ne 0$ remains arbitrary.

Time-Limited Signals

If $ x(t)=0$ for $ \left\vert t\right\vert\geq \Delta t/2$, then

$\displaystyle \Delta t\cdot\Delta \omega \geq \pi $

where $ \Delta \omega $ is as defined above in Eq.$ \,$(C.1).


Proof: See [52, pp. 274-5].

Time-Bandwidth Products are Unbounded Above

We have considered two lower bounds for the time-bandwidth product based on two different definitions of duration in time. In the opposite direction, there is no upper bound on time-bandwidth product. To see this, imagine filtering an arbitrary signal with an allpass filter.C.2 The allpass filter cannot affect bandwidth $ \Delta \omega $, but the duration $ \Delta t$ can be arbitrarily extended by successive applications of the allpass filter.

Next Section:
Sampling Theory
Previous Section:
Fourier Transforms for Continuous/Discrete Time/Frequency