Signals as Vectors
For the DFT, all signals and spectra are length ![]() . A length
. A length ![]() sequence
sequence
![]() can be denoted by
can be denoted by ![]() ,
,
![]() , where
, where ![]() may be
real (
may be
real (
![]() ) or complex (
) or complex (
![]() ). We now wish to regard
). We now wish to regard ![]() as a
vector5.1
as a
vector5.1
![]() in an
in an ![]() dimensional vector space. That is,
each sample
dimensional vector space. That is,
each sample ![]() is regarded as a coordinate in that space.
A vector
is regarded as a coordinate in that space.
A vector
![]() is mathematically a single point in
is mathematically a single point in
![]() -space represented by a list of coordinates
-space represented by a list of coordinates
![]() called an
called an ![]() -tuple. (The
notation
-tuple. (The
notation ![]() means the same thing as
means the same thing as ![]() .) It can be interpreted
geometrically as an arrow in
.) It can be interpreted
geometrically as an arrow in ![]() -space from the origin
-space from the origin
![]() to the point
to the point
![]() .
.
We define the following as equivalent:
The reader comfortable with vectors, vector addition, and vector subtraction may skip to §5.6.
An Example Vector View: 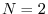
Consider the example two-sample signal
![]() graphed in
Fig.5.1.
graphed in
Fig.5.1.
Under the geometric interpretation of a length ![]() signal, each sample is a
coordinate in the
signal, each sample is a
coordinate in the ![]() dimensional space. Signals which are only two
samples long are not terribly interesting to hear,5.2 but they are easy to
plot geometrically.
dimensional space. Signals which are only two
samples long are not terribly interesting to hear,5.2 but they are easy to
plot geometrically.
Next Section:
Vector Addition
Previous Section:
The DFT








![\includegraphics[scale=0.7]{eps/vec2d}](http://www.dsprelated.com/josimages_new/mdft/img689.png)











