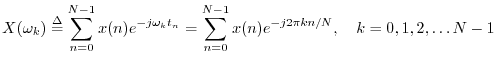DSPRelated.com
Free Books
   Free Books    Mathematics of the DFT  

The DFT

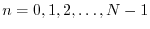For a length $ N$ complex sequence $ x(n)$, $ n=0,1,2,\ldots,N-1$, the discrete Fourier transform (DFT) is defined by

$\displaystyle X(\omega_k) \isdef \sum_{n=0}^{N-1}x(n) e^{-j\omega_k t_n} = \sum_{n=0}^{N-1}x(n) e^{-j 2\pi kn/N}, \quad k=0,1,2,\ldots N-1 $

\begin{eqnarray*} t_n &\isdef & nT = \mbox{$n$th sampling instant (sec)} \\ \om... ...sdef & 2\pi f_s/N = \mbox{frequency sampling interval (rad/sec)} \end{eqnarray*}

We are now in a position to have a full understanding of the transform kernel:

$\displaystyle e^{-j\omega_k t_n} = \cos(\omega_k t_n) - j \sin(\omega_k t_n) $

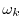
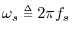
The kernel consists of samples of a complex sinusoid at $ N$ discrete frequencies $ \omega_k$ uniformly spaced between 0 and the sampling rate $ \omega_s \isdeftext 2\pi f_s$. All that remains is to understand the purpose and function of the summation over $ n$ of the pointwise product of $ x(n)$ times each complex sinusoid. 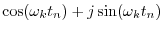We will learn that this can be interpreted as an inner product operation which computes the coefficient of projection of the signal $ x$ onto the complex sinusoid $ \cos(\omega_k t_n) + j \sin(\omega_k t_n)$. 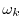As such, $ X(\omega_k)$, the DFT at frequency $ \omega_k$, is a measure of the amplitude and phase of the complex sinusoid which is present in the input signal $ x$ at that frequency. This is the basic function of all linear transform summations (in discrete time) and integrals (in continuous time) and their kernels.

Next Section:
Signals as Vectors
Previous Section:
Sinusoid Problems