Free Books
   Free Books    Mathematics of the DFT  

Unbiased Cross-Correlation

Recall that the cross-correlation operator is cyclic (circular) since $ n+l$ is interpreted modulo $ N$. In practice, we are normally interested in estimating the acyclic cross-correlation between two signals. For this (more realistic) case, we may define instead the unbiased cross-correlation

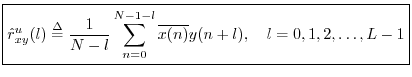
$\displaystyle \zbox {{\hat r}^u_{xy}(l) \isdef \frac{1}{N-l}\sum_{n=0}^{N-1-l} \overline{x(n)} y(n+l),\quad l = 0,1,2,\ldots,L-1} $

where we choose $ L\ll N$ (e.g., $ L\approx\sqrt{N}$) in order to have enough lagged products $ \overline{x(n)} y(n+l)$ at the highest lag $ L-1$ so that a reasonably accurate average is obtained. Note that the summation stops at $ n=N-l-1$ to avoid cyclic wrap-around of $ n$ modulo $ N$. The term ``unbiased'' refers to the fact that the expected value8.9[33] of $ {\hat r}^u_{xy}(l)$ is the true cross-correlation $ r_{xy}(l)$ of $ x$ and $ y$ (assumed to be samples from stationary stochastic processes).

An unbiased acyclic cross-correlation may be computed faster via DFT (FFT) methods using zero padding:

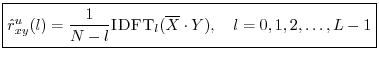
$\displaystyle \zbox {{\hat r}^u_{xy}(l) = \frac{1}{N-l}\hbox{\sc IDFT}_l(\overline{X}\cdot Y), \quad l = 0,1,2,\ldots,L-1} $

where

\begin{eqnarray*} X &=& \hbox{\sc DFT}[\hbox{\sc CausalZeroPad}_{N+L-1}(x)]\\ Y &=& \hbox{\sc DFT}[\hbox{\sc CausalZeroPad}_{N+L-1}(y)]. \end{eqnarray*}

Note that $ x$ and $ y$ belong to $ {\bf C}^N$ while $ X$ and $ Y$ belong to $ {\bf C}^{N+L-1}$. The zero-padding may be causal (as defined in §7.2.8) because the signals are assumed to be be stationary, in which case all signal statistics are time-invariant. As usual when embedding acyclic correlation (or convolution) within the cyclic variant given by the DFT, sufficient zero-padding is provided so that only zeros are ``time aliased'' (wrapped around in time) by modulo indexing.

Cross-correlation is used extensively in audio signal processing for applications such as time scale modification, pitch shifting, click removal, and many others.

Next Section:
Autocorrelation
Previous Section:
Cross-Correlation