Free Books    Mathematics of the DFT  

Cross-Correlation


Definition: The circular cross-correlation of two signals $ x$ and $ y$ in $ {\bf C}^N$ may be defined by

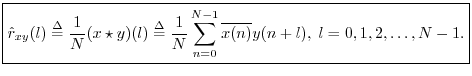
$\displaystyle \zbox {{\hat r}_{xy}(l) \isdef \frac{1}{N}(x\star y)(l) \isdef \frac{1}{N}\sum_{n=0}^{N-1}\overline{x(n)} y(n+l), \; l=0,1,2,\ldots,N-1.} $

(Note that the ``lag'' $ l$ is an integer variable, not the constant $ 1$.) The DFT correlation operator `$ \star$' was first defined in §7.2.5.

The term ``cross-correlation'' comes from statistics, and what we have defined here is more properly called a ``sample cross-correlation.'' That is, $ {\hat r}_{xy}(l)$ is an estimator8.8 of the true cross-correlation $ r_{xy}(l)$ which is an assumed statistical property of the signal itself. This definition of a sample cross-correlation is only valid for stationary stochastic processes, e.g., ``steady noises'' that sound unchanged over time. The statistics of a stationary stochastic process are by definition time invariant, thereby allowing time-averages to be used for estimating statistics such as cross-correlations. For brevity below, we will typically not include ``sample'' qualifier, because all computational methods discussed will be sample-based methods intended for use on stationary data segments.

The DFT of the cross-correlation may be called the cross-spectral density, or ``cross-power spectrum,'' or even simply ``cross-spectrum'':

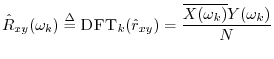
$\displaystyle {\hat R}_{xy}(\omega_k) \isdef \hbox{\sc DFT}_k({\hat r}_{xy}) = \frac{\overline{X(\omega_k)}Y(\omega_k)}{N} $

The last equality above follows from the correlation theorem (§7.4.7).

Next Section:
Unbiased Cross-Correlation
Previous Section:
Phase Response