Free Books    Mathematics of the DFT  

Introduction to Sampling

Inside computers and modern ``digital'' synthesizers, (as well as music CDs), sound is sampled into a stream of numbers. Each sample can be thought of as a number which specifies the positionD.2of a loudspeaker at a particular instant. When sound is sampled, we call it digital audio. The sampling rate used for CDs nowadays is 44,100 samples per second. That means when you play a CD, the speakers in your stereo system are moved to a new position 44,100 times per second, or once every 23 microseconds. Controlling a speaker this fast enables it to generate any sound in the human hearing range because we cannot hear frequencies higher than around 20,000 cycles per second, and a sampling rate more than twice the highest frequency in the sound guarantees that exact reconstruction is possible from the samples.

Reconstruction from Samples--Pictorial Version

Figure D.1 shows how a sound is reconstructed from its samples. Each sample can be considered as specifying the scaling and location of a sinc function. The discrete-time signal being interpolated in the figure is a digital rectangular pulse:

$\displaystyle x = [\dots, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, \dots] $

The sinc functions are drawn with dashed lines, and they sum to produce the solid curve. An isolated sinc function is shown in Fig.D.2. Note the ``Gibb's overshoot'' near the corners of the continuous rectangular pulse in Fig.D.1 due to bandlimiting. (A true continuous rectangular pulse has infinite bandwidth.)

Figure D.1: Summation of weighted sinc functions to create a continuous waveform from discrete-time samples.
\includegraphics[width=\twidth]{eps/SincSum}

Notice that each sinc function passes through zero at every sample instant but the one it is centered on, where it passes through 1.

The Sinc Function

Figure: The sinc function $ \protect$sinc$ (x) \protect\isdef \protect\sin(\pi x)/(\pi x)$.
\includegraphics[width=\twidth]{eps/Sinc}

The sinc function, or cardinal sine function, is the famous ``sine x over x'' curve, and is illustrated in Fig.D.2. For bandlimited interpolation of discrete-time signals, the ideal interpolation kernel is proportional to the sinc function

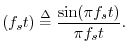
   sinc$\displaystyle (f_st) \isdef \frac{\sin(\pi f_st)}{\pi f_st}. $

where $ f_s$ denotes the sampling rate in samples-per-second (Hz), and $ t$ denotes time in seconds. Note that the sinc function has zeros at all the integers except 0, where it is 1. For precise scaling, the desired interpolation kernel is $ f_s$sinc$ (f_st)$, which has a algebraic area (time integral) that is independent of the sampling rate $ f_s$.

Reconstruction from Samples--The Math

Let $ x_d(n) \isdef x(nT)$ denote the $ n$th sample of the original sound $ x(t)$, where $ t$ is time in seconds. Thus, $ n$ ranges over the integers, and $ T$ is the sampling interval in seconds. The sampling rate in Hertz (Hz) is just the reciprocal of the sampling period, i.e.,

$\displaystyle f_s\isdef \frac{1}{T}. $

To avoid losing any information as a result of sampling, we must assume $ x(t)$ is bandlimited to less than half the sampling rate. This means there can be no energy in $ x(t)$ at frequency $ f_s/2$ or above. We will prove this mathematically when we prove the sampling theorem in §D.3 below.

Let $ X(\omega)$ denote the Fourier transform of $ x(t)$, i.e.,

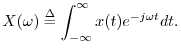
$\displaystyle X(\omega)\isdef \int_{-\infty}^\infty x(t) e^{-j\omega t} dt . $

Then we can say $ x$ is bandlimited to less than half the sampling rate if and only if $ X(\omega)=0$ for all $ \vert\omega\vert\geq\pi f_s$. In this case, the sampling theorem gives us that $ x(t)$ can be uniquely reconstructed from the samples $ x(nT)$ by summing up shifted, scaled, sinc functions:

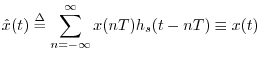
$\displaystyle {\hat x}(t) \isdef \sum_{n=-\infty}^\infty x(nT) h_s(t-nT) \equiv x(t) $

where

$\displaystyle h_s(t) \isdef$   sinc$\displaystyle (f_st) \isdef \frac{\sin(\pi f_st)}{\pi f_st}. $

The sinc function is the impulse response of the ideal lowpass filter. This means its Fourier transform is a rectangular window in the frequency domain. The particular sinc function used here corresponds to the ideal lowpass filter which cuts off at half the sampling rate. In other words, it has a gain of 1 between frequencies 0 and $ f_s/2$, and a gain of zero at all higher frequencies.

The reconstruction of a sound from its samples can thus be interpreted as follows: convert the sample stream into a weighted impulse train, and pass that signal through an ideal lowpass filter which cuts off at half the sampling rate. These are the fundamental steps of digital to analog conversion (DAC). In practice, neither the impulses nor the lowpass filter are ideal, but they are usually close enough to ideal that one cannot hear any difference. Practical lowpass-filter design is discussed in the context of bandlimited interpolation [72].

Next Section:
Aliasing of Sampled Signals
Previous Section:
The Uncertainty Principle