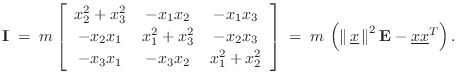Angular Momentum Vector in Matrix Form
The two cross-products in Eq.![]() (B.19) can be written out with the help
of the vector analysis identityB.23
(B.19) can be written out with the help
of the vector analysis identityB.23
where
![$\displaystyle \mathbf{I}\underline{\omega}\eqsp
\left[\begin{array}{ccc}
I_{1...
...begin{array}{c} \omega_1 \\ [2pt] \omega_2 \\ [2pt] \omega_3\end{array}\right]
$](http://www.dsprelated.com/josimages_new/pasp/img2872.png)
The matrix
The vector angular momentum of a rigid body is obtained by summing the angular momentum of its constituent mass particles. Thus,
In summary, the angular momentum vector
![]() is given by the mass
moment of inertia tensor
is given by the mass
moment of inertia tensor
![]() times the angular-velocity vector
times the angular-velocity vector
![]() representing the axis of rotation.
representing the axis of rotation.
Note that the angular momentum vector
![]() does not in general
point in the same direction as the angular-velocity vector
does not in general
point in the same direction as the angular-velocity vector
![]() . We
saw above that it does in the special case of a point mass traveling
orthogonal to its position vector. In general,
. We
saw above that it does in the special case of a point mass traveling
orthogonal to its position vector. In general,
![]() and
and
![]() point
in the same direction whenever
point
in the same direction whenever
![]() is an eigenvector of
is an eigenvector of
![]() , as will be discussed further below (§B.4.16). In this
case, the rigid body is said to be dynamically balanced.B.24
, as will be discussed further below (§B.4.16). In this
case, the rigid body is said to be dynamically balanced.B.24
Next Section:
Simple Example
Previous Section:
Relation of Angular to Linear Momentum