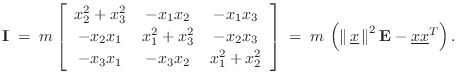Angular Momentum Vector
Like linear momentum, angular momentum is fundamentally a vector in
![]() . The definition of the previous section suffices when the
direction does not change, in which case we can focus only on its
magnitude
. The definition of the previous section suffices when the
direction does not change, in which case we can focus only on its
magnitude ![]() .
.
More generally, let
![]() denote the 3-space coordinates
of a point-mass
denote the 3-space coordinates
of a point-mass ![]() , and let
, and let
![]() denote its velocity
in
denote its velocity
in ![]() . Then the instantaneous angular momentum vector
of the mass relative to the origin (not necessarily rotating about a
fixed axis) is given by
. Then the instantaneous angular momentum vector
of the mass relative to the origin (not necessarily rotating about a
fixed axis) is given by
where
For the special case in which
![]() is orthogonal to
is orthogonal to
![]() , as in Fig.B.4, we have that
, as in Fig.B.4, we have that
![]() points, by the right-hand rule, in the direction of the angular
velocity vector
points, by the right-hand rule, in the direction of the angular
velocity vector
![]() (up out of the page), which is
satisfying. Furthermore, its magnitude is given by
(up out of the page), which is
satisfying. Furthermore, its magnitude is given by
In the more general case of an arbitrary mass velocity vector
![]() , we know from §B.4.12 that the magnitude of
, we know from §B.4.12 that the magnitude of
![]() equals the product of the distance from the axis
of rotation to the mass, i.e.,
equals the product of the distance from the axis
of rotation to the mass, i.e.,
![]() , times the length of
the component of
, times the length of
the component of
![]() that is orthogonal to
that is orthogonal to
![]() , i.e.,
, i.e.,
![]() , as needed.
, as needed.
It can be shown that vector angular momentum, as defined, is conserved.B.22 For example, in an orbit, such as that of the moon around the earth, or that of Halley's comet around the sun, the orbiting object speeds up as it comes closer to the object it is orbiting. (See Kepler's laws of planetary motion.) Similarly, a spinning ice-skater spins faster when pulling in arms to reduce the moment of inertia about the spin axis. The conservation of angular momentum can be shown to result from the principle of least action and the isotrophy of space [270, p. 18].
Angular Momentum Vector in Matrix Form
The two cross-products in Eq.![]() (B.19) can be written out with the help
of the vector analysis identityB.23
(B.19) can be written out with the help
of the vector analysis identityB.23
where
![$\displaystyle \mathbf{I}\underline{\omega}\eqsp
\left[\begin{array}{ccc}
I_{1...
...begin{array}{c} \omega_1 \\ [2pt] \omega_2 \\ [2pt] \omega_3\end{array}\right]
$](http://www.dsprelated.com/josimages_new/pasp/img2872.png)
The matrix
The vector angular momentum of a rigid body is obtained by summing the angular momentum of its constituent mass particles. Thus,
In summary, the angular momentum vector
![]() is given by the mass
moment of inertia tensor
is given by the mass
moment of inertia tensor
![]() times the angular-velocity vector
times the angular-velocity vector
![]() representing the axis of rotation.
representing the axis of rotation.
Note that the angular momentum vector
![]() does not in general
point in the same direction as the angular-velocity vector
does not in general
point in the same direction as the angular-velocity vector
![]() . We
saw above that it does in the special case of a point mass traveling
orthogonal to its position vector. In general,
. We
saw above that it does in the special case of a point mass traveling
orthogonal to its position vector. In general,
![]() and
and
![]() point
in the same direction whenever
point
in the same direction whenever
![]() is an eigenvector of
is an eigenvector of
![]() , as will be discussed further below (§B.4.16). In this
case, the rigid body is said to be dynamically balanced.B.24
, as will be discussed further below (§B.4.16). In this
case, the rigid body is said to be dynamically balanced.B.24
Next Section:
Mass Moment of Inertia Tensor
Previous Section:
Angular Momentum