Mass Moment of Inertia Tensor
As derived in the previous section, the moment of inertia
tensor, in 3D Cartesian coordinates, is a three-by-three matrix
![]() that can be multiplied by any angular-velocity vector to
produce the corresponding angular momentum vector for either a point
mass or a rigid mass distribution. Note that the origin of the
angular-velocity vector
that can be multiplied by any angular-velocity vector to
produce the corresponding angular momentum vector for either a point
mass or a rigid mass distribution. Note that the origin of the
angular-velocity vector
![]() is always fixed at
is always fixed at
![]() in the space
(typically located at the center of mass). Therefore, the moment of
inertia tensor
in the space
(typically located at the center of mass). Therefore, the moment of
inertia tensor
![]() is defined relative to that origin.
is defined relative to that origin.
The moment of inertia tensor can similarly be used to compute the
mass moment of inertia for any normalized angular velocity
vector
![]() as
as
Since rotational energy is defined as
We can show Eq.
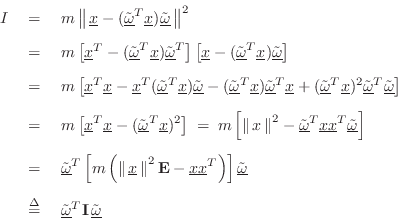
where again
![]() denotes the three-by-three identity matrix, and
denotes the three-by-three identity matrix, and
which agrees with Eq.
For a collection of ![]() masses
masses ![]() located at
located at
![]() , we
simply sum over their masses to add up the moments of inertia:
, we
simply sum over their masses to add up the moments of inertia:
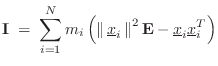
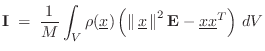
Simple Example
Consider a mass ![]() at
at
![]() . Then the mass moment of inertia
tensor is
. Then the mass moment of inertia
tensor is
![$\displaystyle \mathbf{I}\eqsp m \left(\left\Vert\,\underline{x}\,\right\Vert^2\...
...ay}{ccc}
0 & 0 & 0\\ [2pt]
0 & 1 & 0\\ [2pt]
0 & 0 & 1
\end{array}\right].
$](http://www.dsprelated.com/josimages_new/pasp/img2891.png)
![\begin{displaymath}
I \eqsp \underline{\tilde{\omega}}^T\mathbf{I}\,\underline{\...
...{array}{c} 1 \\ [2pt] 0 \\ [2pt] 0\end{array}\right]m \eqsp 0.
\end{displaymath}](http://www.dsprelated.com/josimages_new/pasp/img2893.png)
![$\displaystyle I \eqsp \underline{\tilde{\omega}}^T\mathbf{I}\,\underline{\tilde...
...]
\left[\begin{array}{c} 0 \\ [2pt] 1 \\ [2pt] 0\end{array}\right] \eqsp m x^2
$](http://www.dsprelated.com/josimages_new/pasp/img2895.png)
Example with Coupled Rotations
Now let the mass ![]() be located at
be located at
![]() so that
so that
![\begin{eqnarray*}
\mathbf{I}&=& m \left(\left\Vert\,\underline{x}\,\right\Vert^2...
... & 0\\ [2pt]
-1 & 1 & 0\\ [2pt]
0 & 0 & 2
\end{array}\right].
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img2897.png)
We expect
![]() to yield zero for the moment of inertia, and
sure enough
to yield zero for the moment of inertia, and
sure enough
![]() . Similarly, the vector angular
momentum is zero, since
. Similarly, the vector angular
momentum is zero, since
![]() .
.
For
![]() , the result is
, the result is
![\begin{displaymath}
\mathbf{I}\eqsp
\begin{array}{r}\left[\begin{array}{ccc} 1 ...
...egin{array}{c} 1 \\ [2pt] 0 \\ [2pt] 0\end{array}\right]m = m,
\end{displaymath}](http://www.dsprelated.com/josimages_new/pasp/img2902.png)
Off-Diagonal Terms in Moment of Inertia Tensor
This all makes sense, but what about those ![]() off-diagonal terms in
off-diagonal terms in
![]() ? Consider the vector angular momentum (§B.4.14):
? Consider the vector angular momentum (§B.4.14):
![$\displaystyle \underline{L}\eqsp \mathbf{I}\,\underline{\omega}\eqsp
m\left[\b...
...begin{array}{c} \omega_1 \\ [2pt] \omega_2 \\ [2pt] \omega_3\end{array}\right]
$](http://www.dsprelated.com/josimages_new/pasp/img2907.png)
Next Section:
Principal Axes of Rotation
Previous Section:
Angular Momentum Vector



















