Avoiding Discontinuities When Changing Delay
We have seen examples (e.g., Figures 4.16 and 4.18)
of the general fact that every Lagrange interpolator provides an integer
delay at frequency
![]() , except when the interpolator gain
is zero at
, except when the interpolator gain
is zero at
![]() . This is true for any interpolator
implemented as a real FIR filter, i.e., as a linear combination of signal
samples using real coefficients.5.4Therefore, to avoid a relatively large discontinuity in phase delay (at
high frequencies) when varying the delay over time, the requested
interpolation delay should stay within a half-sample range of some fixed
integer, irrespective of interpolation order. This provides that the
requested delay stays within the ``capture zone'' of a single integer at
half the sampling rate. Of course, if the delay varies by more than one
sample, there is no way to avoid the high-frequency discontinuity in the
phase delay using Lagrange interpolation.
. This is true for any interpolator
implemented as a real FIR filter, i.e., as a linear combination of signal
samples using real coefficients.5.4Therefore, to avoid a relatively large discontinuity in phase delay (at
high frequencies) when varying the delay over time, the requested
interpolation delay should stay within a half-sample range of some fixed
integer, irrespective of interpolation order. This provides that the
requested delay stays within the ``capture zone'' of a single integer at
half the sampling rate. Of course, if the delay varies by more than one
sample, there is no way to avoid the high-frequency discontinuity in the
phase delay using Lagrange interpolation.
Even-order Lagrange interpolators have an integer at the midpoint of their central one-sample range, so they spontaneously offer a one-sample variable delay free of high-frequency discontinuities.
Odd-order Lagrange interpolators, on the other hand, must be shifted by
![]() sample in either direction in order to be centered about an
integer delay. This can result in stability problems if the
interpolator is used in a feedback loop, because the interpolation gain
can exceed 1 at some frequency when venturing outside the central
one-sample range (see §4.2.11 below).
sample in either direction in order to be centered about an
integer delay. This can result in stability problems if the
interpolator is used in a feedback loop, because the interpolation gain
can exceed 1 at some frequency when venturing outside the central
one-sample range (see §4.2.11 below).
In summary, discontinuity-free interpolation ranges include
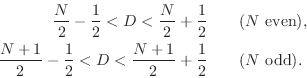
Wider delay ranges, and delay ranges not centered about an integer
delay, will include a phase discontinuity in the delay response (as a
function of delay) which is largest at frequency
![]() , as
seen in Figures 4.16 and 4.18.
, as
seen in Figures 4.16 and 4.18.
Next Section:
Lagrange Frequency Response Magnitude Bound
Previous Section:
Lagrange Frequency Response Examples



















