Bridge Transmittance
The bridge transmittance is the filter needed for the signal path from the vibrating string to the resonant acoustic body.
Since the bridge velocity equals the string endpoint velocity (a ``series'' connection), the velocity transmittance is simply
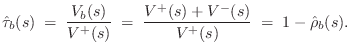
If the bridge is rigid, then its motion becomes a velocity input to the acoustic resonator. In principle, there are three such velocity inputs for each point along the bridge. However, it is typical in stringed instrument models to consider only the vertical transverse velocity on the string as significant, which results in one (vertical) driving velocity at the base of the bridge. In violin models (§9.6), the use of a ``sound post'' on one side of the bridge and ``bass bar'' on the other strongly suggests supporting a rocking motion along the bridge.
Next Section:
Digitizing Bridge Reflectance
Previous Section:
Bridge Reflectance




















