Digitization of the Damped-Spring Plectrum
Applying the bilinear transformation (§7.3.2) to the reflectance
![]() in Eq.
in Eq.![]() (9.23) (including damping) yields the
following first-order digital force-reflectance filter:
(9.23) (including damping) yields the
following first-order digital force-reflectance filter:
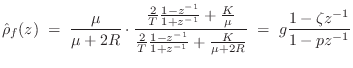
The transmittance filter is again
Next Section:
Feathering
Previous Section:
Plectrum Damping








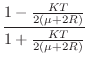 (digital
(digital 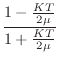 (digital zero)
(digital zero)











