Bilinear Transformation
The bilinear transform is defined by the substitution
where
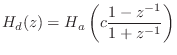
It can be seen that analog dc (![]() ) maps to digital dc (
) maps to digital dc (![]() ) and
the highest analog frequency (
) and
the highest analog frequency (![]() ) maps to the highest digital
frequency (
) maps to the highest digital
frequency (![]() ). It is easy to show that the entire
). It is easy to show that the entire ![]() axis
in the
axis
in the ![]() plane (where
plane (where
![]() ) is mapped exactly
once around the unit circle in the
) is mapped exactly
once around the unit circle in the ![]() plane (rather than
summing around it infinitely many times, or ``aliasing'' as it does in
ordinary sampling). With
plane (rather than
summing around it infinitely many times, or ``aliasing'' as it does in
ordinary sampling). With ![]() real and positive, the left-half
real and positive, the left-half ![]() plane maps to the interior of the unit circle, and the right-half
plane maps to the interior of the unit circle, and the right-half ![]() plane maps outside the unit circle. This means stability is
preserved when mapping a continuous-time transfer function to
discrete time.
plane maps outside the unit circle. This means stability is
preserved when mapping a continuous-time transfer function to
discrete time.
Another valuable property of the bilinear transform is that
order is preserved. That is, an ![]() th-order
th-order ![]() -plane transfer
function carries over to an
-plane transfer
function carries over to an ![]() th-order
th-order ![]() -plane transfer function.
(Order in both cases equals the maximum of the degrees of the
numerator and denominator polynomials [449]).8.6
-plane transfer function.
(Order in both cases equals the maximum of the degrees of the
numerator and denominator polynomials [449]).8.6
The constant ![]() provides one remaining degree of freedom which can be used
to map any particular finite frequency from the
provides one remaining degree of freedom which can be used
to map any particular finite frequency from the ![]() axis in the
axis in the ![]() plane to a particular desired location on the unit circle
plane to a particular desired location on the unit circle
![]() in the
in the ![]() plane. All other frequencies will be warped. In
particular, approaching half the sampling rate, the frequency axis
compresses more and more. Note that at most one resonant frequency can be
preserved under the bilinear transformation of a mass-spring-dashpot
system. On the other hand, filters having a single transition frequency,
such as lowpass or highpass filters, map beautifully under the bilinear
transform; one simply uses
plane. All other frequencies will be warped. In
particular, approaching half the sampling rate, the frequency axis
compresses more and more. Note that at most one resonant frequency can be
preserved under the bilinear transformation of a mass-spring-dashpot
system. On the other hand, filters having a single transition frequency,
such as lowpass or highpass filters, map beautifully under the bilinear
transform; one simply uses ![]() to map the cut-off frequency where it
belongs, and the response looks great. In particular, ``equal ripple'' is
preserved for optimal filters of the elliptic and Chebyshev types because
the values taken on by the frequency response are identical in both cases;
only the frequency axis is warped.
to map the cut-off frequency where it
belongs, and the response looks great. In particular, ``equal ripple'' is
preserved for optimal filters of the elliptic and Chebyshev types because
the values taken on by the frequency response are identical in both cases;
only the frequency axis is warped.
The bilinear transform is often used to design digital filters from analog prototype filters [343]. An on-line introduction is given in [449].
Finite Difference Approximation vs. Bilinear Transform
Recall that the Finite Difference Approximation (FDA) defines the
elementary differentiator by
![]() (ignoring the
scale factor
(ignoring the
scale factor ![]() for now), and this approximates the ideal transfer
function
for now), and this approximates the ideal transfer
function ![]() by
by
![]() . The bilinear transform
calls instead for the transfer function
. The bilinear transform
calls instead for the transfer function
![]() (again
dropping the scale factor) which introduces a pole at
(again
dropping the scale factor) which introduces a pole at ![]() and gives
us the recursion
and gives
us the recursion
![]() .
Note that this new pole is right on the unit circle and is therefore
undamped. Any signal energy at half the sampling rate will circulate
forever in the recursion, and due to round-off error, it will tend to
grow. This is therefore a potentially problematic revision of the
differentiator. To get something more practical, we need to specify
that the filter frequency response approximate
.
Note that this new pole is right on the unit circle and is therefore
undamped. Any signal energy at half the sampling rate will circulate
forever in the recursion, and due to round-off error, it will tend to
grow. This is therefore a potentially problematic revision of the
differentiator. To get something more practical, we need to specify
that the filter frequency response approximate
![]() over a
finite range of frequencies
over a
finite range of frequencies
![]() , where
, where
![]() , above which we allow the response to ``roll off''
to zero. This is how we pose the differentiator problem in terms of
general purpose filter design (see §8.6) [362].
, above which we allow the response to ``roll off''
to zero. This is how we pose the differentiator problem in terms of
general purpose filter design (see §8.6) [362].
To understand the properties of the finite difference approximation in the
frequency domain, we may look at the properties of its ![]() -plane
to
-plane
to ![]() -plane mapping
-plane mapping
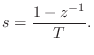
Setting ![]() to 1 for simplicity and solving the FDA mapping for z gives
to 1 for simplicity and solving the FDA mapping for z gives
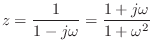
Under the FDA, analog and digital frequency axes coincide well enough at
very low frequencies (high sampling rates), but at high frequencies
relative to the sampling rate, artificial damping is introduced as
the image of the ![]() axis diverges away from the unit circle.
axis diverges away from the unit circle.
While the bilinear transform ``warps'' the frequency axis, we can say the FDA ``doubly warps'' the frequency axis: It has a progressive, compressive warping in the direction of increasing frequency, like the bilinear transform, but unlike the bilinear transform, it also warps normal to the frequency axis.
Consider a point traversing the upper half of the unit circle in the z
plane, starting at ![]() and ending at
and ending at ![]() . At dc, the FDA is
perfect, but as we proceed out along the unit circle, we diverge from the
. At dc, the FDA is
perfect, but as we proceed out along the unit circle, we diverge from the
![]() axis image and carve an arc somewhere out in the image of the
right-half
axis image and carve an arc somewhere out in the image of the
right-half ![]() plane. This has the effect of introducing an artificial
damping.
plane. This has the effect of introducing an artificial
damping.
Consider, for example, an undamped mass-spring system. There will be a
complex conjugate pair of poles on the ![]() axis in the
axis in the ![]() plane. After
the FDA, those poles will be inside the unit circle, and therefore damped
in the digital counterpart. The higher the resonance frequency, the larger
the damping. It is even possible for unstable
plane. After
the FDA, those poles will be inside the unit circle, and therefore damped
in the digital counterpart. The higher the resonance frequency, the larger
the damping. It is even possible for unstable ![]() -plane poles to be mapped
to stable
-plane poles to be mapped
to stable ![]() -plane poles.
-plane poles.
In summary, both the bilinear transform and the FDA preserve order,
stability, and positive realness. They are both free of aliasing, high
frequencies are compressively warped, and both become ideal at dc, or as
![]() approaches
approaches ![]() . However, at frequencies significantly above
zero relative to the sampling rate, only the FDA introduces artificial
damping. The bilinear transform maps the continuous-time frequency axis in
the
. However, at frequencies significantly above
zero relative to the sampling rate, only the FDA introduces artificial
damping. The bilinear transform maps the continuous-time frequency axis in
the ![]() (the
(the ![]() axis) plane precisely to the discrete-time frequency
axis in the
axis) plane precisely to the discrete-time frequency
axis in the ![]() plane (the unit circle).
plane (the unit circle).
Next Section:
Application of the Bilinear Transform
Previous Section:
Finite Difference Approximation








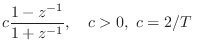 (typically)
(typically)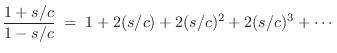
![\includegraphics[width=3in]{eps/lfdacirc}](http://www.dsprelated.com/josimages_new/pasp/img1678.png)












